마르코프 모델(Markov Models)
지금까지 우리는 관찰한 일부 정보를 바탕으로 확률에 대한 질문을 살펴보았다. 이런 패러다임에서는 시간의 차원이 전혀 표현되지 않는다. 그러나 예측과 같은 많은 작업은 시간 차원에 의존한다. 시간 변수를 나타내기 위해 새 변수 X를 생성하고 관심 있는 이벤트에 따라 이를 변경한다. 즉, Xₜ는 현재 이벤트이고 Xₜ₊₁는 다음 이벤트이다. 미래의 사건을 예측할 수 있기 위해, 우리는 Markov 모델을 사용할 것이다.
마르코프 가정(Markov Assumption)
마르코프 가정은 현재 상태(state)가 유한하고 고정된 수의 이전 상태(state)들에만 의존한다는 가정이다. 이것은 우리에게 중요하다.
날씨를 예측하는 작업을 생각해 보자. 이론적으로 우리는 지난해의 모든 데이터를 사용하여 내일의 날씨를 예측할 수 있다. 그러나 이는 필요한 계산 능력과 365일 전 날씨를 기반으로 내일 날씨의 조건부 확률에 대한 정보가 없기 때문에 실행 불가능하다. 마르코프 가정을 사용하여 이전 상태(예: 내일 날씨를 예측할 때 고려할 이전 날짜 수)를 제한하여 작업을 관리하기 쉽게 만든다. 이는 관심 확률에 대한 더 대략적인 근사치를 얻을 수 있음을 의미하지만 이는 종종 우리의 요구에는 충분하다. 또한 마지막 이벤트 정보를 기반으로 Markov 모델을 사용할 수 있다(예: 오늘 날씨를 기반으로 내일 날씨 예측).
마르코프 체인(Markov Chain)
마르코프 체인은 각 변수의 분포가 마르코프 가정을 따르는 일련의 무작위 변수이다. 즉, 체인의 각 이벤트는 이전 이벤트의 확률에 따라 발생한다. 마르코프 체인 구축을 시작하려면 현재 이벤트의 가능한 값을 기반으로 다음 이벤트의 확률 분포를 지정하는 전환 모델(transition model)이 필요하다.

이 예에서는 오늘 맑음을 기준으로 내일 맑을 확률은 0.8이다. 화창한 날이 지나면 화창한 날이 올 확률이 높기 때문에 이것은 합리적이다. 만약 오늘 비가 온다면 내일 비가 올 확률은 0.7이다. 비 오는 날이 연달아 올 확률이 높기 때문이다. 이 전환 모델을 사용하면 Markov 체인을 샘플링할 수 있다. 비가 오거나 맑은 날로 시작한 다음, 오늘 날씨를 고려하여 맑거나 비가 올 확률을 기준으로 다음 날을 샘플링한다. 그런 다음 내일을 기준으로 내일모레의 확률을 조건으로 지정하여 마르코프 체인을 만든다:
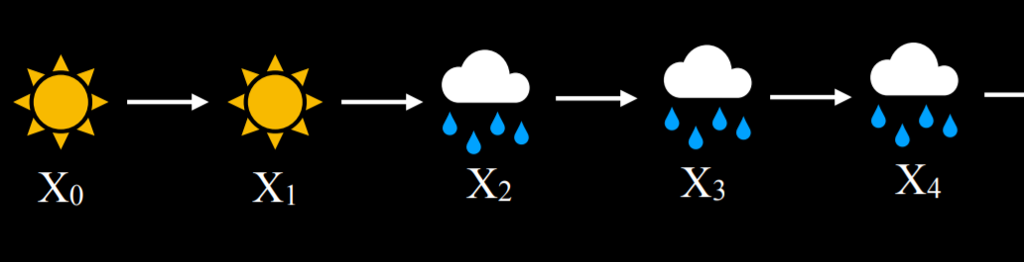
이 마르코프 체인이 주어지면 이제 "4일 연속 비가 올 확률은 얼마입니까?"와 같은 질문에 대답할 수 있다. 다음은 Markov 체인을 코드에서 구현하는 방법의 예시이다.
from pomegranate import *
# Define starting probabilities
start = DiscreteDistribution({
"sun": 0.5,
"rain": 0.5
})
# Define transition model
transitions = ConditionalProbabilityTable([
["sun", "sun", 0.8],
["sun", "rain", 0.2],
["rain", "sun", 0.3],
["rain", "rain", 0.7]
], [start])
# Create Markov chain
model = MarkovChain([start, transitions])
# Sample 50 states from chain
print(model.sample(50))은닉 마르코프 모델(Hidden Markov Models)
은닉 마르코프 모델은 마르코프 모델의 한 유형으로 관찰된 이벤트를 생성하는 숨겨진 상태(state)를 갖는 시스템이다. 이는 때때로 AI가 세계에 대한 일부 측정을 갖고 있지만 세계의 정확한 상태에 접근할 수 없다는 것을 의미한다. 이러한 경우 세계의 상태를 숨겨진 상태(hidden state)라고 하며 AI가 액세스 할 수 있는 모든 데이터는 관찰(observations)이다. 이에 대한 몇 가지 예는 다음과 같다.
- 미지의 영역을 탐험하는 로봇의 경우 숨겨진 상태는 로봇의 위치이고 관찰은 로봇 센서에 의해 기록된 데이터이다.
- 음성 인식에서 숨겨진 상태는 말한 단어이고 관찰은 오디오 파형이다.
- 웹사이트에서 사용자 참여를 측정할 때 숨겨진 상태는 사용자의 참여 정도이고 관찰은 웹사이트 또는 앱 분석이다.
다음 예시를 보자. 우리의 AI는 날씨(숨겨진 상태)를 추론하고 싶어 하지만 얼마나 많은 사람들이 우산을 가져왔는지 기록하는 실내 카메라에만 액세스 할 수 있다. 다음은 이러한 확률을 나타내는 센서 모델 (방출(emission) 모델 이라고도 함)이다:

이 모델에서는 날씨가 맑으면 사람들이 건물에 우산을 가져오지 않을 가능성이 가장 높다. 비가 오면 사람들이 우산을 건물로 가져올 가능성이 높다. 사람들이 우산을 가지고 왔는지 아닌지를 관찰함으로써 우리는 바깥 날씨가 어떤지 합리적인 확률로 예측할 수 있다.
센서 마르코프 가정(Sensor Markov Assumption)
증거 변수는 해당 상태(corresponding state)에만 의존한다는 가정이다.
예를 들어, 우리 모델의 경우 사람들이 사무실에 우산을 가져오는지 여부는 날씨에만 의존한다고 가정하자. 예를 들어 더 성실하고 비를 싫어하는 사람들은 날씨가 맑을 때에도 어디에서나 우산을 가지고 다닐 수 있고 모든 사람의 성격을 안다면 모델에 더 많은 데이터를 추가할 수 있기 때문에 이것이 반드시 완전한 진실을 반영하는 것은 아니다. 그러나 센서 마르코프 가정은 숨겨진 상태만이 관측에 영향을 미친다고 가정하여 이러한 데이터를 무시한다.
은닉 마르코프 모델은 두 개의 레이어가 있는 마르코프 체인으로 표현될 수 있다. 최상위 레이어인 변수 X는 숨겨진 상태를 나타낸다. 맨 아래 레이어인 변수 E는 증거, 즉 우리가 관찰한 내용을 나타낸다.

은닉 마르코프 모델을 기반으로 여러 작업을 수행할 수 있다.
- 필터링(Filtering): 처음부터 지금까지의 관찰을 바탕으로 현재 상태에 대한 확률 분포를 계산한다. 예를 들어, 사람들이 시작부터 오늘까지 언제 우산을 가져왔는지에 대한 정보가 주어지면 오늘 비가 올지 여부에 대한 확률 분포를 생성한다.
- 예측(Prediction): 시작부터 지금까지의 관찰을 바탕으로 미래 상태에 대한 확률 분포를 계산한다.
- 평활화(Smoothing): 처음부터 지금까지의 관찰을 통해 과거 상태에 대한 확률 분포를 계산한다. 예를 들어, 사람들이 오늘 우산을 가져왔다는 점을 고려하여 어제 비가 올 확률을 계산한다.
- 가장 가능성이 높은 설명: 처음부터 지금까지의 관찰을 바탕으로 가장 가능성이 높은 일련의 사건을 계산한다.
가능성이 가장 높은 설명 작업은 음성 인식과 같은 프로세스에서 사용될 수 있다. 여기서 AI는 여러 파형을 기반으로 이러한 파형을 가져온 가장 가능성 있는 단어 또는 음절의 시퀀스를 추론한다. 다음은 파이썬으로 만든 가장 가능성이 높은 설명 작업에 사용할 은닉 마르코프 모델이다:
from pomegranate import *
# Observation model for each state
sun = DiscreteDistribution({
"umbrella": 0.2,
"no umbrella": 0.8
})
rain = DiscreteDistribution({
"umbrella": 0.9,
"no umbrella": 0.1
})
states = [sun, rain]
# Transition model
transitions = numpy.array(
[[0.8, 0.2], # Tomorrow's predictions if today = sun
[0.3, 0.7]] # Tomorrow's predictions if today = rain
)
# Starting probabilities
starts = numpy.array([0.5, 0.5])
# Create the model
model = HiddenMarkovModel.from_matrix(
transitions, states, starts,
state_names=["sun", "rain"]
)
model.bake()
우리 모델에는 센서 모델(sensor model)과 전환 모델(transition model)이 모두 있다. 은닉 마르코프 모델에는 둘 다 필요하다. 다음 코드에서 우리는 사람들이 건물에 우산을 가져왔는지 여부에 대한 일련의 관찰을 확인하고, 이 시퀀스를 기반으로 모델을 실행하여 가장 가능성 있는 설명(예: 가장 가능성이 높은 날씨 시퀀스)을 생성하고 출력한다. 아마도 이러한 관찰 패턴이 발생했을 것이다):
from model import model
# Observed data
observations = [
"umbrella",
"umbrella",
"no umbrella",
"umbrella",
"umbrella",
"umbrella",
"umbrella",
"no umbrella",
"no umbrella"
]
# Predict underlying states
predictions = model.predict(observations)
for prediction in predictions:
print(model.states[prediction].name)
이 경우 프로그램의 출력은 비, 비, 맑음, 비, 비, 비, 비, 맑음, 맑음이 된다. 이 출력은 사람들이 건물에 우산을 가져오거나 가져오지 않는 것을 관찰한 결과, 가장 가능성이 높은 날씨 패턴을 나타낸다.
이렇게 챕터 3인 불확실성(uncertainty)에 대해 알아봤다. 다음 챕터에는 최적화에 대해 알아볼 것이다.
'인공지능 > 인공지능개론' 카테고리의 다른 글
| [AI] Learning (5-3) (0) | 2024.06.25 |
|---|---|
| [AI] Learning (5-2) (0) | 2024.06.24 |
| [AI] Uncertainty (3-2) (2) | 2024.06.24 |
| [AI] Learning (5-1) (0) | 2024.06.21 |
| [AI] Optimization (4-3) (1) | 2024.06.11 |



