회귀(Regression)
회귀는 입력 지점을 연속 값, 일부 실수 값에 매핑하는 함수의 지도 학습 작업이다. 이는 분류 문제가 입력을 이산 값(비 또는 비 안 옴)에 매핑한다는 점에서 분류와 차이가 있다.
예를 들어, 회사는 회귀 분석을 사용하여 광고에 지출된 비용이 판매로 벌어들인 돈을 예측하는 방법에 대한 질문에 답할 수 있다. 이 경우, 관찰된 함수 f(advertising)는 광고에 지출된 일부 돈에 따른 관찰된 수입을 나타낸다(함수는 두 개 이상의 입력 변수를 사용할 수 있음에 유의하자). 이것이 우리가 시작하는 데이터이다. 이 데이터를 사용하여 함수 f의 동작을 근사화하려고 시도하는 가설 함수 h(advertising)를 제시하려고 한다. h는 관찰 유형을 분리하는 것이 아니라 입력을 기반으로 출력 값을 예측하는 것이 목표인 선을 생성한다.

손실함수(Loss Functions)
손실 함수는 이전 파트에서 결정 규칙에 의해 손실된 효용을 수량화하는 방법이다. 예측이 정확하지 않을수록 손실이 커진다.
분류 문제의 경우, 0-1 손실 함수를 사용할 수 있다.
- L (실제, 예측):
- 0이 실제인 경우 = 예측됨
- 그 외 1개
즉, 이 함수는 예측이 정확하지 않을 때 값을 얻고 예측이 정확할 때(즉, 관찰 값과 예측 값이 일치할 때) 값을 얻지 않는다.

위의 예에서 값이 0인 날은 날씨를 정확하게 예측한 날이다(비가 오는 날은 선 아래에 있고 비가 내리지 않는 날은 선 위에 있다). 그러나 선 아래로 비가 내리지 않은 날과 선 위로 비가 내린 날은 우리가 예측하지 못한 날이다. 우리는 각각에 1의 값을 부여하고 이를 합산하여 결정 경계가 얼마나 손실이 있는지에 대한 경험적 추정을 얻는다.
L₁ 및 L₂ 손실 함수는 연속 값을 예측할 때 사용할 수 있다. 이 경우, 우리는 각 예측이 관찰된 값과 얼마나 다른지 정량화하는 데 관심이 있다. 관측값의 절댓값이나 제곱값에서 예측값을 뺀 값(즉, 예측값이 관측값과 얼마나 멀리 떨어져 있는지)을 취하여 이를 수행한다.
- L₁: L (실제, 예측) = |실제 - 예측|
- L₂ : L (실제, 예측) = (실제 - 예측) ²
목표에 가장 적합한 손실 함수를 선택할 수 있다. L₂ 는 차이를 제곱하기 때문에 L₁보다 이상값에 더 가혹하게 페널티를 적용한다. L₁는 각 관찰 지점에서 회귀선의 예측 지점까지의 거리를 합산하여 시각화할 수 있다:

과적합(Overfitting)
과적합은 모델이 훈련 데이터에 너무 잘 맞아서 다른 데이터 세트로 일반화하지 못하는 경우이다. 이런 의미에서 손실 함수는 양날의 검이 된다. 아래 두 예에서는 손실 함수가 최소화되어 손실이 0이 된다. 그러나 새 데이터에 잘 맞을 가능성은 낮다.

예를 들어 왼쪽 그래프에서 화면 하단 빨간색 점 옆에 있는 점은 비(파란색) 일 가능성이 높다. 하지만 과적합 모델에서는 No Rain(빨간색)으로 분류된다. 오른쪽에서는 회귀선에서의 거리가 0(실제=예측)이 되어 일반화에 실패해 버린다.
정규화(Regularization)
정규화는 더 간단하고 일반적인 가설을 선호하기 위해 더 복잡한 가설에 불이익을 주는 프로세스이다. 과적합을 방지하기 위해 정규화를 사용한다.
정규화에서는 손실과 복잡성 측정값을 합산하여 가설 함수 h의 비용을 추정한다.
비용 (h) = 손실 (h) + λ복잡도(h)
람다(λ)는 비용 함수의 복잡성에 대한 페널티를 얼마나 강력하게 조정하는 데 사용할 수 있는 상수이다. λ가 높을수록 비용이 많이 드는 복잡성이 커진다.
모델이 과적합되었는지 테스트하는 한 가지 방법은 홀드아웃 교차 검증(Holdout Cross Validation)을 사용하는 것이다. 이 기술에서는 모든 데이터를 훈련 세트와 테스트 세트라는 두 개로 나눈다. 훈련 세트에서 학습 알고리즘을 실행한 다음 테스트 세트의 데이터를 얼마나 잘 예측하는지 확인한다. 여기서의 아이디어는 훈련에 사용되지 않은 데이터를 테스트함으로써 학습이 얼마나 잘 일반화되는지 측정할 수 있다는 것이다.
홀드아웃 교차 검증의 단점은 평가 목적으로 사용되기 때문에 데이터의 절반으로 모델을 훈련할 수 없다는 것이다. 이를 처리하는 방법은 k -Fold Cross-Validation을 사용하는 것이다. 이 과정에서 우리는 데이터를 k개의 세트로 나눕니다. 우리는 훈련을 k번 실행하는데, 매번 하나의 데이터 세트를 제외하고 이를 테스트 세트로 사용한다. 우리는 모델에 대해 k개의 서로 다른 평가를 수행하여 데이터 손실 없이 모델이 일반화되는 방식을 평균화하고 추정할 수 있다.
사이킷런(scikit-learn)
Python의 경우와 마찬가지로 기계 학습 알고리즘을 편리하게 사용할 수 있는 여러 라이브러리가 있다. 그러한 라이브러리 중 하나가 scikit-learn이다.
예를 들어 맨 위에서 위조지폐의 데이터세트를 다운로드하여 사용해 보자.
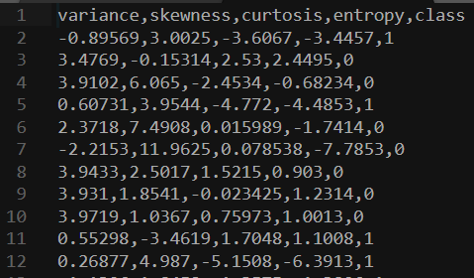
왼쪽 4개 열은 지폐가 진짜인지 위조인지 예측하는 데 사용할 수 있는 데이터이다. 이는 인간이 제공한 외부 데이터로 0과 1로 코딩된다. 이제 이 데이터 세트에 대해 모델을 훈련하고 가능한지 확인할 수 있다. 새 지폐가 진짜인지 아닌지 예측해 보자.
import csv
import random
from sklearn import svm
from sklearn.linear_model import Perceptron
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
# model = KNeighborsClassifier(n_neighbors=1)
# model = svm.SVC()
model = Perceptron()라이브러리를 가져온 후 사용할 모델을 선택할 수 있다. 나머지 코드는 동일하게 유지된다. SVC는 Support Vector Classifier(지원 벡터 머신으로 알려져 있음)를 나타낸다. KNeighborsClassifier는 k-이웃 전략을 사용하며 고려해야 할 이웃 수를 입력으로 요구한다.
# Read data in from file
with open("banknotes.csv") as f:
reader = csv.reader(f)
next(reader)
data = []
for row in reader:
data.append({
"evidence": [float(cell) for cell in row[:4]],
"label": "Authentic" if row[4] == "0" else "Counterfeit"
})
# Separate data into training and testing groups
holdout = int(0.40 * len(data))
random.shuffle(data)
testing = data[:holdout]
training = data[holdout:]
# Train model on training set
X_training = [row["evidence"] for row in training]
y_training = [row["label"] for row in training]
model.fit(X_training, y_training)
# Make predictions on the testing set
X_testing = [row["evidence"] for row in testing]
y_testing = [row["label"] for row in testing]
predictions = model.predict(X_testing)
# Compute how well we performed
correct = 0
incorrect = 0
total = 0
for actual, predicted in zip(y_testing, predictions):
total += 1
if actual == predicted:
correct += 1
else:
incorrect += 1
# Print results
print(f"Results for model {type(model).__name__}")
print(f"Correct: {correct}")
print(f"Incorrect: {incorrect}")
print(f"Accuracy: {100 * correct / total:.2f}%")알고리즘을 실행하는 수동 버전은 banknotes0.py에서 찾을 수 있다. 알고리즘은 유사한 방식으로 자주 사용되므로 scikit-learn에는 코드를 더욱 간결하고 사용하기 쉽게 만드는 추가 기능이 포함되어 있으며 이 버전은 banknotes1.py에서 찾을 수 있다.
여기까지 회귀와 손실함수, 과적합, 정규화, 사이킷런까지 알아봤다. 다음에는 챕터 5의 나머지 파트인 강화 학습과 비지도 학습을 배울 것이다.
'인공지능 > 인공지능개론' 카테고리의 다른 글
| [AI] Neural Networks (6-1) (1) | 2024.06.28 |
|---|---|
| [AI] Learning (5-3) (0) | 2024.06.25 |
| [AI] Uncertainty (3-3) (2) | 2024.06.24 |
| [AI] Uncertainty (3-2) (2) | 2024.06.24 |
| [AI] Learning (5-1) (0) | 2024.06.21 |



