기계 학습(Machine learning)
머신러닝은 명시적인 지침이 아닌 데이터를 컴퓨터에 제공해 준다. 컴퓨터는 이러한 데이터를 사용하여 패턴을 인식하는 방법을 학습하고 스스로 작업을 실행하게 된다.
지도 학습(Supervised learning)
지도 학습은 컴퓨터가 입력-출력 쌍의 데이터 세트를 기반으로 입력을 출력으로 매핑하는 기능을 학습하는 작업이다.
분류(Classification)
지도 학습에는 여러 작업이 있으며 그 중 하나가 분류이다 . 이는 함수가 입력을 이산 출력에 매핑하는 작업이다.
예를 들어, 특정 날짜의 습도와 기압에 대한 정보가 주어지면(입력), 컴퓨터는 그날 비가 올지 여부를 결정한다(출력). 컴퓨터는 비가 왔는지 여부에 따라 습도와 기압이 이미 매핑되어 있는 여러 날의 데이터 세트에 대한 교육을 수행한 후 이 작업을 수행하게 된다.
이 작업을 공식으로 만들어보자. 우리는 함수 f (습도, 압력)가 입력을 Rain 또는 No Rain 중 하나의 이산 값에 매핑하는 자연을 관찰한다. 이 함수는 우리에게 숨겨져 있으며 아마도 우리가 접근할 수 없는 다른 많은 변수의 영향을 받을 것이다. 우리의 목표는 함수 f 의 동작을 근사화할 수 있는 함수 h (습도, 압력)를 만드는 것이다.
이러한 작업은 습도와 비(입력) 차원에 날짜를 표시하고, 해당 날짜에 비가 오면 각 데이터 포인트를 파란색으로, 해당 날짜에 비가 내리지 않으면 빨간색으로 표시하여(출력) 시각화할 수 있다. 흰색 데이터 포인트에는 입력만 있고 컴퓨터는 출력을 파악해야 한다.

최근접 이웃 분류 (Nearest Neighbor Classification)
위에서 설명한 것과 같은 작업을 해결하는 한 가지 방법은 문제의 변수에 가장 가까운 관찰 값을 할당하는 것이다.
예를 들어, 위 그래프의 흰색 점은 파란색으로 표시된다. 가장 가까운 관측 점도 파란색이기 때문이다. 이것은 때때로 잘 작동할 수도 있지만 반드시는 아닌 이유를 아래 그래프를 보며 알아보자.
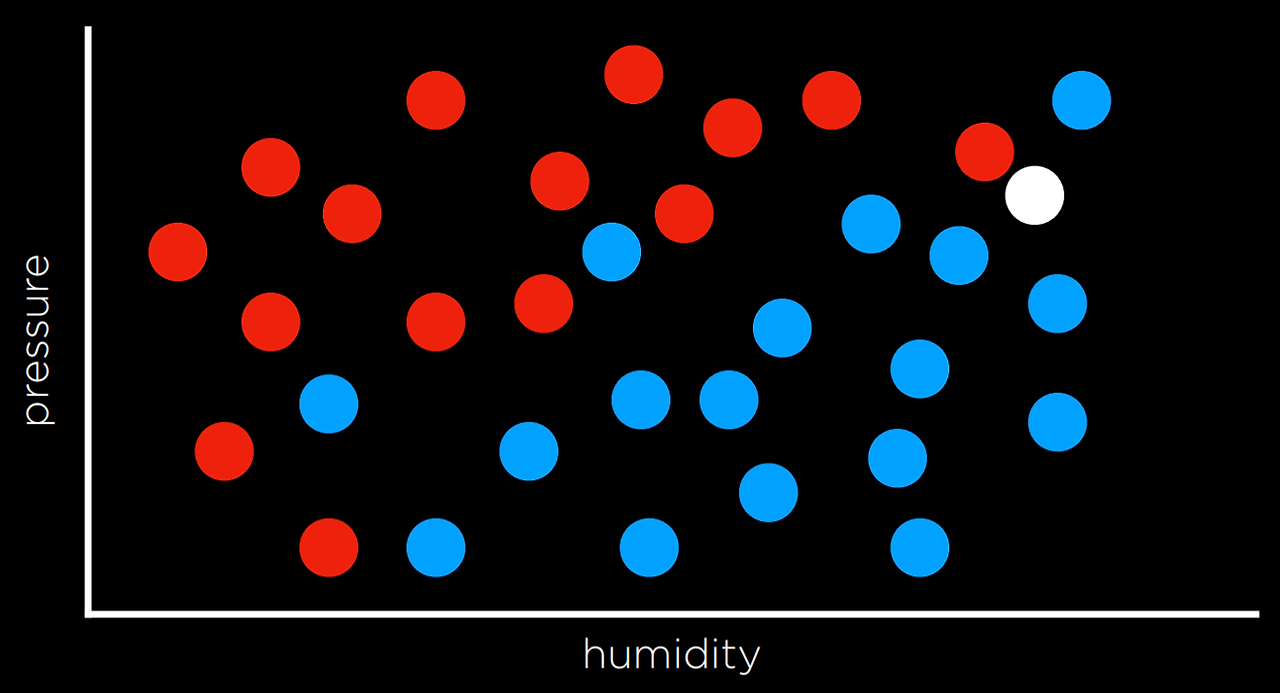
동일한 전략에 따라 흰색 점은 빨간색으로 표시되어야 한다. 왜냐하면 가장 가까운 관찰도 빨간색이기 때문이다. 그러나 더 넓게 보면 주변의 다른 관측치 대부분이 파란색인 것처럼 보인다. 이는 가장 가까운 관측치가 빨간색임에도 불구하고 이 경우 파란색이 더 나은 예측이라는 직관을 제공할 수 있다.
최근접이웃 분류의 한계를 극복하는 한 가지 방법은 k-최근접이웃 분류를 사용하는 것이다. 여기서 점은 k개의 최근접이웃 중 가장 빈번한 색상을 기준으로 색상이 지정된다.k가 무엇인지 결정하는 것은 만든 사람 마음이다.
예를 들어, 3-최근접 이웃 분류를 사용하면 위의 흰색 점은 파란색으로 표시되며 이는 직관적으로 더 나은 결정처럼 보인다.
k-최근접 이웃 분류의 단점은 순진한 접근 방식을 사용하면 알고리즘이 문제의 지점까지 모든 단일 지점의 거리를 측정해야 하며, 이는 계산 비용이 많이 든다는 것이다. 이는 이웃을 더 빠르게 찾을 수 있는 데이터 구조를 사용하거나 관련 없는 관측값을 정리함으로써 속도를 높일 수 있다.
퍼셉트론 학습(Perceptron Learning)
최근접 이웃 전략과 달리 분류 문제를 해결하는 또 다른 방법은 데이터 전체를 살펴보고 결정 경계를 만드는 것이다. 2차원 데이터에서는 두 가지 유형의 관측값 사이에 선을 그릴 수 있다. 모든 추가 데이터 포인트는 해당 데이터 포인트가 표시된 선의 측면을 기준으로 분류된다.

이 접근 방식의 단점은 데이터가 지저분하고, 선을 긋고 실수 없이 클래스를 두 개의 관찰로 깔끔하게 나눌 수 있는 경우가 거의 없다. 종종 우리는 관측치를 정확하게 분리하는 경계를 그리면서 타협할 것이지만 여전히 때때로 관측치를 잘못 분류할 것이다.
이 경우, input으로 x₁ = 습도, x₂ = 압력이 그날 비가 올지 여부에 대한 예측을 출력하는 가설 함수 h(x₁, x₂)에서 제공된다. 관찰이 결정 경계의 어느 쪽에 속하는지 확인하여 이를 수행한다. 공식적으로 이 함수는 상수를 추가하여 각 입력에 가중치를 부여하고 다음 형식의 선형 방정식으로 끝난다.
- 비 w₀ + w₁x₁ + w₂x₂ ≥ 0
- 그렇지 않으면 비가 내리지 않습니다
종종 출력 변수는 1과 0으로 코딩한다. 여기서 방정식이 0보다 큰 값을 산출하면 출력은 1(비)이고 그렇지 않으면 0(비 없음)이 된다.
가중치와 값은 숫자의 시퀀스인 벡터로 표현한다(파이썬에서는 목록이나 튜플에 저장할 수 있음). 우리는 가중치 벡터 w(w₀, w₁, w₂ )와 입력 벡터 x: (1, x₁, x₂ )를 생성하며, 최상의 가중치 벡터를 얻는 것이 기계 학습 알고리즘의 목표이다.
- 가중치 벡터: w(w₀, w₁, w₂ )
- 입력벡터: x(1, x₁, x₂)
이제 두 벡터를 내적 하면 다음 식이 나온다. w₀ + w₁x₁ + w2x₂.
참고로 입력 벡터의 첫 번째 값은 1이다. 왜냐하면 가중치 벡터 w₀를 곱할 때 이를 상수로 유지하기를 원하기 때문이다.
따라서 가설 함수를 다음과 같이 표현할 수 있다:

알고리즘의 목표는 최상의 가중치 벡터를 찾는 것이므로 알고리즘이 새 데이터를 만나면 현재 가중치를 업데이트한다. 이는 퍼셉트론 학습 규칙을 사용하여 수행한다.

이 규칙에서 중요한 점은 각 데이터 포인트에 대해 가중치를 조정하여 함수를 더 정확하게 만든다는 것이다.
우리의 요점에 그다지 중요하지 않은 세부 사항은 각 가중치가 그 자체에 괄호 안의 일부 값을 더한 값과 동일하게 설정된다는 것이다.
위 식에서 y는 관측값을 나타내고 가설 함수는 추정치를 나타낸다.
- 동일한 경우, 괄호 안의 값은 0이므로 가중치는 변경되지 않는다. wᵢ = wᵢ + 0
- 과소평가한 경우(Rain이 관측된 동안 No Rain 호출), 괄호 안의 값은 1이 되고 가중치는 학습 계수 α로 조정된 xᵢ 값만큼 증가한다. wᵢ = wᵢ + αxᵢ
- 과대평가한 경우(비가 없는 동안 Rain 호출), 괄호 안의 값은 -1이 되고 가중치는 α로 스케일링된 x 값만큼 감소한다. wᵢ = wᵢ + (-αxᵢ)
α가 높을수록 각각의 새로운 이벤트가 가중치에 미치는 영향이 더 강해진다.
이 프로세스의 결과는 추정값이 일부 임계값을 초과하면 0에서 1로 전환되는 임계값 함수이다.
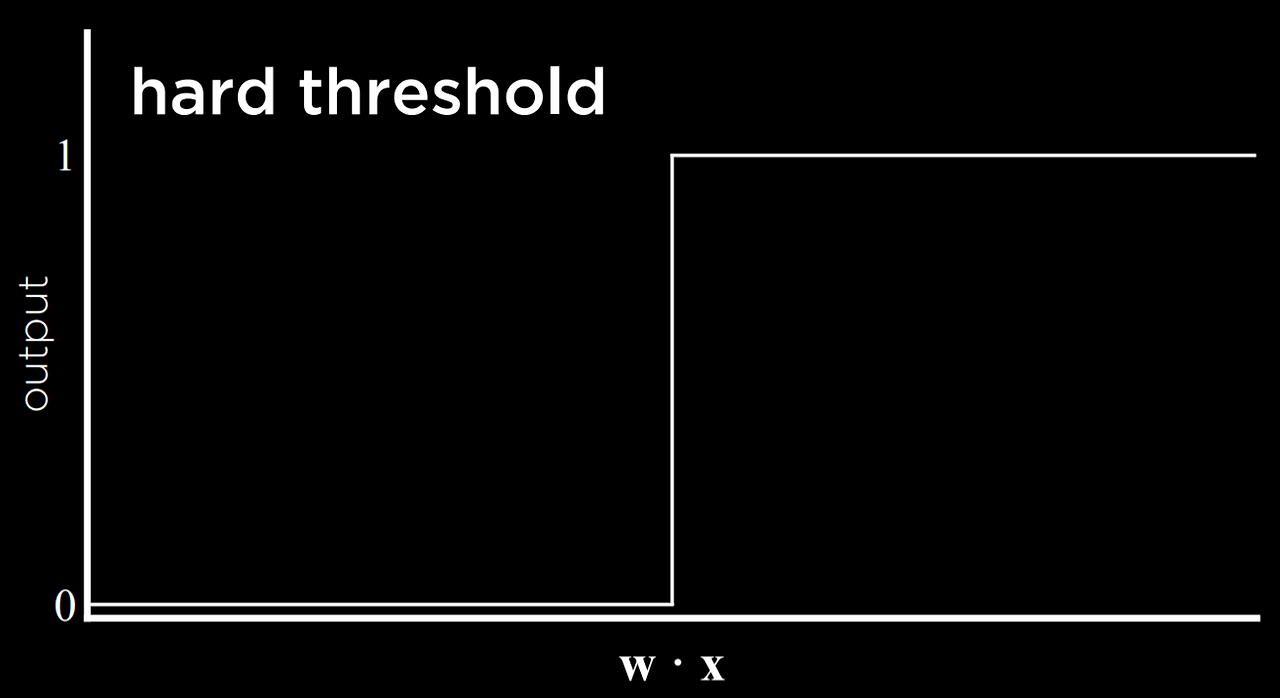
이러한 유형의 함수의 문제점은 무조건 0 또는 1의 결괏값만 같을 수 있기 때문에 불확실성을 표현할 수 없다는 것이다.
이 함수는 하드 임계값을 사용힌다. 따라서, 이 문제를 해결하는 방법은 소프트 임계값을 사용하는 로지스틱 함수를 사용하는 것이다. 로지스틱 함수는 0과 1 사이의 실수를 산출할 수 있으며 이는 추정치에 대한 신뢰도를 표현한다. 값이 1에 가까울수록 비가 올 가능성이 높아진다.

보조 벡터 머신(Support Vector Machine)
최근접 회귀 및 선형 회귀 외에도 분류에 대한 또 다른 접근 방식은 보조 벡터 머신(Support Vector Machine)이다. 이 접근 방식은 데이터를 분리할 때 최선의 결정을 내리기 위해 결정 경계 근처의 추가 벡터(서포트 벡터)를 사용한다. 아래 예를 보자.

모든 결정 경계는 실수 없이 데이터를 분리한다는 점에서 작동한다. 그러나 그들은 똑같이 좋을까? 왼쪽에 있는 두 결정 경계는 일부 관찰과 매우 가깝다. 이는 한 그룹과 약간만 다른 새로운 데이터 포인트가 다른 그룹으로 잘못 분류될 수 있음을 의미한다. 이와는 대조적으로, 가장 오른쪽의 결정 경계는 각 그룹과 가장 큰 거리를 유지하므로 그 내에서 가장 많은 변형 여지를 제공한다. 분리하는 두 그룹에서 가능한 한 멀리 있는 이러한 유형의 경계를 최대 마진 구분 기호 라고 한다.
서포트 벡터 머신의 또 다른 이점은 비선형 결정 경계뿐만 아니라 아래와 같이 2차원 이상에서 결정 경계를 나타낼 수 있다는 것이다.

분류 문제를 해결하는 방법에는 여러 가지가 있으며 어느 쪽도 항상 다른 쪽보다 낫지는 않다. 각각에는 단점이 있으며 특정 상황에서는 다른 것보다 더 유용할 수 있다. 다음에는 회귀파트를 알아보도록 하자.
'인공지능 > 인공지능개론' 카테고리의 다른 글
| [AI] Uncertainty (3-3) (2) | 2024.06.24 |
|---|---|
| [AI] Uncertainty (3-2) (2) | 2024.06.24 |
| [AI] Optimization (4-3) (1) | 2024.06.11 |
| [AI] Optimization (4-2) (0) | 2024.06.05 |
| [AI] Optimization (4-1) (1) | 2024.06.05 |


