베이즈 망(Bayesian Networks)
베이즈 망은 확률 변수 간의 종속성을 나타내는 데이터 구조이다. 베이즈 망에는 다음과 같은 특성이 있다.
- 방향이 있는 그래프이다.
- 그래프의 각 노드는 랜덤 변수를 나타낸다.
- X에서 Y로 향하는 화살표는 X가 Y의 부모임을 나타낸다. 즉, Y의 확률 분포는 X의 값에 따라 달라지게 된다.
- 각 노드 X는 확률 분포 P( X | Parents(X) )를 갖는다.
약속 시간에 맞춰 도착하는지 여부에 영향을 미치는 변수가 포함된 베이즈 망의 예를 생각해 보자.

위에서부터 차례대로 분석해 보자.
- Rain은 이 네트워크의 루트 노드이다. 이는 확률 분포가 이전 사건에 의존하지 않음을 의미한다. 이 예시에서 Rain은 다음 확률 분포를 사용하여 { none, light, heavy } 값을 취할 수 있는 무작위 변수이다.

- Maintenance은 { yes, no } 값을 사용하여 열차 선로 유지 관리가 있는지 여부를 인코딩한다. Rain은 Maintenance의 상위 노드이다. 이는 Maintenance의 확률 분포가 Rain의 영향을 받는다는 의미이다.

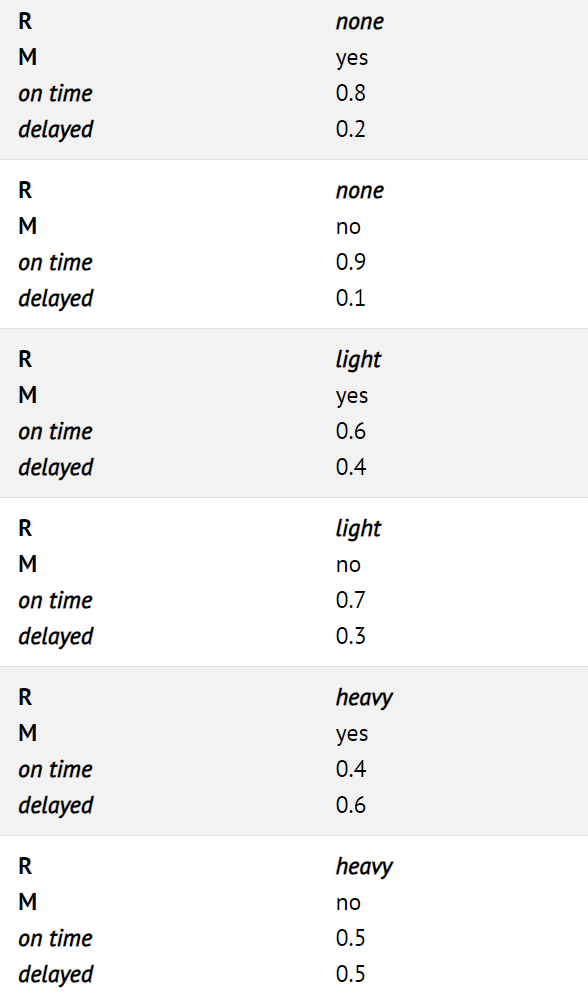
- Train은 열차가 정시에 도착하는지 지연되는지 여부를 인코딩하는 변수로, { on time, delayed } 값을 사용한다. Train에는 Maintenance와 Rain 모두에서 이를 가리키는 화살표가 있다. 이는 둘 다 Train의 상위이고 해당 값이 Train의 확률 분포에 영향을 미친다는 것을 의미한다.
- Appointment는 약속 참석 여부를 나타내는 무작위 변수로, { attend, miss } 값을 사용한다. 유일한 부모는 Train이다. 베이지안 네트워크에 대한 이 점은 주목할 만하다. 부모에는 직접적인 관계만 포함된다. Maintenance가 기차의 정시에 도착하는지 여부에 영향을 미치고, Train이 정시에 도착하는지 여부가 우리가 약속에 참석하는지 여부에 영향을 미치는 것은 사실이다. 그러나 결국 약속에 참석할 확률에 직접적인 영향을 미치는 것은 기차가 정시에 도착했는지 여부이며, 이것이 베이즈 망에 표현된다. 예를 들어, 기차가 정시에 도착했다면 폭우가 내리고 선로 유지 관리가 필요할 수 있지만 약속 시간에 도착했는지 여부에는 아무런 영향을 미치지 않는다.
예를 들어, 유지 보수가 없고 약간의 비가 내리는 날 기차가 연착되었을 때 회의를 놓칠 확률, 즉 P( light , no, delayed, miss)를 찾으려면 다음을 계산하면 된다: P(light) P(no | light) P(delayed | light, no) P(miss | delayed). 각 개별 확률의 값은 위의 확률 분포에서 찾을 수 있으며, P( no, light, Delayed, Miss )를 생성하기 위해 위 값들을 곱해야 한다.
추론(Inference)
지난 챕터에서는 수반(entailment)을 통한 추론에 대해 살펴보았었다. 이는 우리가 이미 가지고 있는 정보를 바탕으로 새로운 정보를 확실하게 결론 내릴 수 있다는 것을 의미한다. 그러나 확률을 기반으로 새로운 정보를 추론할 수도 있다. 이를 통해 새로운 정보를 확실하게 알 수는 없지만 일부 값에 대한 확률 분포를 파악할 수 있다. 추론에는 여러 속성이 있다.
- 쿼리 X : 확률 분포를 계산하려는 변수.
- 증거 변수 E : 사건 e에 대해 관찰된 하나 이상의 변수. 예를 들어, light rain이 오는 것을 관찰했을 수 있으며, 이 관찰은 기차가 지연될 확률을 계산하는 데 도움이 된다.
- 숨겨진 변수 Y : 쿼리가 아니며 관찰되지 않은 변수. 예를 들어, 기차역에 서서 비가 오는지 관찰할 수 있지만, 도로 아래에 있는 선로에 유지 관리가 있는지는 알 수 없다. 따라서 이 상황에서는 유지 관리가 숨겨진 변수가 된다.
- 목표: P ( X | e )를 계산한다. 예를 들어 약한 비가 내린다는 증거 e를 기반으로 Train 변수(쿼리)의 확률 분포를 계산한다.
예를 들어, 우리는 light rain + no maintenance를 증거로 약속 변수의 확률 분포를 계산해 보자. 즉, 비가 약간 내리고 선로 유지 관리가 없다는 것을 알고 있으며 약속에 참석하고 약속을 놓칠 확률 P(Appointment | light, no)를 알아내야 한다.
이전 파트인 결합 확률에서 우리는 약속 확률 변수의 가능한 값을 비율로 표현하여 P(Appointment | light, no)를 α P(Appointment | light, no)로 다시 쓸 수 있다는 것을 알고 있다.
상위 변수가 Rain이나 Maintenance가 아닌 Train 변수인 경우, 약속의 확률 분포를 어떻게 계산할 수 있을까? 여기서는 소외화를 사용할 것이다. 따라서 P(Appointment, light, no) 값 = α[P(Appointment, light, no, delayed) + P(Appointment, light, no, on time)]값이다.
열거에 의한 추론(Inference by Enumeration)
열거에 의한 추론은 관찰된 증거 e와 일부 숨겨진 변수 Y가 주어졌을 때 변수 X의 확률 분포를 찾는 프로세스이다.

이 방정식에서 X는 쿼리 변수를 나타내고, e는 관찰된 증거를 나타내고, y는 숨겨진 변수의 모든 값을 나타내며, α는 결과를 정규화하여 합이 1이 되는 확률이 되도록 한다. 방정식을 풀어 말하면, e가 주어졌을 때 X의 확률 분포는 X와 e의 정규화된 확률 분포와 동일하다는 뜻이다. 이 분포를 얻기 위해 X, e, y의 정규화된 확률을 합산한다. 여기서 y는 매번 숨겨진 변수 Y의 다른 값을 취한다.
확률적 추론 과정을 쉽게 하기 위해 Python에는 여러 라이브러리가 존재한다. 위의 데이터가 코드로 어떻게 표현되는지 알아보기 위해 pomegranate 라이브러리를 살펴보자.
먼저 노드를 생성하고 각 노드에 대한 확률 분포를 제공한다.
from pomegranate import *
# Rain node has no parents
rain = Node(DiscreteDistribution({
"none": 0.7,
"light": 0.2,
"heavy": 0.1
}), name="rain")
# Track maintenance node is conditional on rain
maintenance = Node(ConditionalProbabilityTable([
["none", "yes", 0.4],
["none", "no", 0.6],
["light", "yes", 0.2],
["light", "no", 0.8],
["heavy", "yes", 0.1],
["heavy", "no", 0.9]
], [rain.distribution]), name="maintenance")
# Train node is conditional on rain and maintenance
train = Node(ConditionalProbabilityTable([
["none", "yes", "on time", 0.8],
["none", "yes", "delayed", 0.2],
["none", "no", "on time", 0.9],
["none", "no", "delayed", 0.1],
["light", "yes", "on time", 0.6],
["light", "yes", "delayed", 0.4],
["light", "no", "on time", 0.7],
["light", "no", "delayed", 0.3],
["heavy", "yes", "on time", 0.4],
["heavy", "yes", "delayed", 0.6],
["heavy", "no", "on time", 0.5],
["heavy", "no", "delayed", 0.5],
], [rain.distribution, maintenance.distribution]), name="train")
# Appointment node is conditional on train
appointment = Node(ConditionalProbabilityTable([
["on time", "attend", 0.9],
["on time", "miss", 0.1],
["delayed", "attend", 0.6],
["delayed", "miss", 0.4]
], [train.distribution]), name="appointment")
모든 노드를 추가한 다음에, 노드 사이에 간선을 추가하여 어떤 노드가 다른 노드의 부모인지 설명하여 모델을 만든다(베이즈 망은 노드 사이에 화살표가 있는 노드로 구성된 유향 그래프라는 점을 기억하자).
# Create a Bayesian Network and add states
model = BayesianNetwork()
model.add_states(rain, maintenance, train, appointment)
# Add edges connecting nodes
model.add_edge(rain, maintenance)
model.add_edge(rain, train)
model.add_edge(maintenance, train)
model.add_edge(train, appointment)
# Finalize model
model.bake()
이제 특정 사건이 발생할 가능성이 얼마나 되는지 묻기 위해 관심 있는 값으로 모델을 실행한다. 이 예에서는 비가 내리지 않고, 선로 유지 관리가 없고, 기차가 정시에 운행하여 우리가 회의에 도착하는 확률이 얼마나 되는지 묻는다.
# Calculate probability for a given observation
probability = model.probability([["none", "no", "on time", "attend"]])
print(probability)
반면에, 관찰된 증거가 주어진 경우 모든 변수에 대한 확률 분포를 제공하기 위해 프로그램을 사용할 수 있다. 다음의 경우에는 열차가 delayed 되었음을 알 수 있다. 이 정보를 바탕으로 Rain, Maintenance 및 Appointment 변수의 확률 분포를 계산하고 출력한다.
# Calculate predictions based on the evidence that the train was delayed
predictions = model.predict_proba({
"train": "delayed"
})
# Print predictions for each node
for node, prediction in zip(model.states, predictions):
if isinstance(prediction, str):
print(f"{node.name}: {prediction}")
else:
print(f"{node.name}")
for value, probability in prediction.parameters[0].items():
print(f" {value}: {probability:.4f}")샘플링(Sampling)
샘플링은 근사 추론 기술 중 하나이다. 샘플링에서는 각 변수가 확률 분포에 따른 값으로 샘플링된다.
예를 들어, 주사위를 사용한 샘플링을 사용하여 분포를 생성하려면 주사위를 여러 번 굴리고 매번 얻은 값을 기록하면 된다. 주사위를 600번 굴렸다고 가정해 보자. 대략 100이 되는 1이 나온 횟수를 세고 나머지 값인 2~6에 대해 반복한다. 그런 다음 각 개수를 총 굴린 수로 나눈다. 이는 주사위를 굴리는 값의 대략적인 분포를 생성한다. 한편으로는 각 값이 1/6의 발생 확률(정확한 확률)을 갖는 결과를 얻을 가능성은 없지만 그와 유사한 결과를 갖게 된다.
다시 위에서의 예시를 보자. Rain 변수 샘플링으로 시작하면 none 값은 0.7의 확률로 생성되고 light 값은 0.2의 확률로 생성되며 Heavy 값은 0.1의 확률로 생성된다. 우리가 얻은 샘플링 값이 none이라고 가정하자. Maintenance 변수에 도달하면 이를 샘플링하지만 Rain이 none인 확률 분포에서만 샘플링한다. 이는 이미 샘플링된 결과이기 때문이다. 우리는 모든 노드를 통해 계속해서 그렇게 진행할 것이다. 이제 하나의 표본이 있고 이 과정을 여러 번 반복하면 분포가 생성된다. 이제 P(Train = on time)가 무엇인지 같은 질문에 대답하려면, Train 변수가 on time 값을 갖는 샘플 수를 계산하고 결과를 총 샘플 수로 나눌 수 있다. 이런 식으로 우리는 P( Train = on time )에 대한 대략적인 확률을 생성했다.
P( Rain = light | Train = on time )와 같은 조건부 확률과 관련된 질문에 답할 수도 있다. 이 경우 Train 값이 time에 맞지 않는 모든 샘플을 무시하고 이전과 같이 진행하면 된다. Train = on time 인 샘플 중 Rain = light 변수가 있는 샘플 수를 계산한 다음 Train = on time 인 샘플의 총 개수로 나눈다.
코드에서는 sampling 함수를 generate_sample()로 정의하자.
import pomegranate
from collections import Counter
from model import model
def generate_sample():
# Mapping of random variable name to sample generated
sample = {}
# Mapping of distribution to sample generated
parents = {}
# Loop over all states, assuming topological order
for state in model.states:
# If we have a non-root node, sample conditional on parents
if isinstance(state.distribution, pomegranate.ConditionalProbabilityTable):
sample[state.name] = state.distribution.sample(parent_values=parents)
# Otherwise, just sample from the distribution alone
else:
sample[state.name] = state.distribution.sample()
# Keep track of the sampled value in the parents mapping
parents[state.distribution] = sample[state.name]
# Return generated sample
return sample이제 열차가 지연되는 경우의 약속 변수의 확률 분포인 P(Appointment | Train = delayed)를 계산하기 위해 다음 코드를 수행한다.
# Rejection sampling
# Compute distribution of Appointment given that train is delayed
N = 10000
data = []
# Repeat sampling 10,000 times
for i in range(N):
# Generate a sample based on the function that we defined earlier
sample = generate_sample()
# If, in this sample, the variable of Train has the value delayed, save the sample. Since we are interested interested in the probability distribution of Appointment given that the train is delayed, we discard the sampled where the train was on time.
if sample["train"] == "delayed":
data.append(sample["appointment"])
# Count how many times each value of the variable appeared. We can later normalize by dividing the results by the total number of saved samples to get the approximate probabilities of the variable that add up to 1.
print(Counter(data))
위의 샘플링 예에서는 우리가 가지고 있는 증거와 일치하지 않는 샘플을 폐기했었다. 이는 사실 비효율적이다. 이 문제를 해결하는 한 가지 방법은 다음 단계를 사용하여 가능성 가중치를 적용하는 것이다.
- 증거 변수의 값을 수정하는 것부터 시작하자.
- 베이즈망 안의 조건부 확률을 사용하여 증거가 아닌 변수를 샘플링한다.
- 가능성(모든 증거가 발생할 확률)을 기준으로 각 샘플에 가중치를 부여한다.
예를 들어 열차가 정시에 도착했다는 관측이 있는 경우, 이전과 같이 샘플링을 시작한다. 우리는 확률 분포를 고려하여 Rain 값을 샘플링한 다음 유지 관리를 수행하지만, Train에 도달하면 항상 관찰된 값을 제공한다(우리의 경우에는 on time). 그런 다음 Train = on time 주어진 확률 분포를 기반으로 약속을 진행하고 샘플링한다. 이제 이 표본이 존재하므로 표본화된 부모를 고려하여 관측 변수의 조건부 확률로 가중치를 부여한다. 즉, Rain을 샘플링하고 light를 얻고 Maintenance를 샘플링하고 yes를 얻은 경우, 이 샘플에 P(Train = on time | light, yes)를 기준으로 가중치를 부여한다.
여기까지 베이즈망과 샘플링을 알아봤다. 다음에는 마르코프 모델을 사용하여 시간의 차원도 고려해 보자.
'인공지능 > 인공지능개론' 카테고리의 다른 글
| [AI] Learning (5-2) (0) | 2024.06.24 |
|---|---|
| [AI] Uncertainty (3-3) (2) | 2024.06.24 |
| [AI] Learning (5-1) (0) | 2024.06.21 |
| [AI] Optimization (4-3) (1) | 2024.06.11 |
| [AI] Optimization (4-2) (0) | 2024.06.05 |



