최적화(Optimization)
최적화는 가능한 옵션 집합에서 최상의 옵션을 선택하는 것이다. 우리는 이미 minimax 알고리즘과 같이 가능한 최상의 옵션을 찾으려고 노력한 문제에 직면했으며 오늘은 훨씬 더 광범위한 문제를 해결하는 데 사용할 수 있는 도구에 대해 알아볼 것이다.
지역 탐색(Local search)
지역 검색은 단일 노드를 유지하고 이웃 노드로 이동하여 검색하는 검색 알고리즘이다. 이 유형의 알고리즘은 이전에 본 검색 유형과 다르다.
예를 들어 미로 해결에서 우리는 목표에 이르는 가장 빠른 길을 찾고 싶지만, 지역 검색은 질문에 대한 최선의 답을 찾는 데 관심이 있다.
즉 현재 상황에서 얼마나 좋은 움직임을 알려주는가(like 체스).
종종 지역 검색은 최적은 아니지만 계산 능력을 보존하면서 "충분히 좋은 (예를 들면 별점 5점 만점에 4.5점? 정도의) " 답변을 제공한다.
아래 지역 검색 문제의 예를 봐보자. 설정된 위치에 4채의 집이 있다. 우리는 두 개의 병원을 짓고 각 집에서 병원까지의 거리를 최소화하고 싶다. 어떻게 해야 할까?
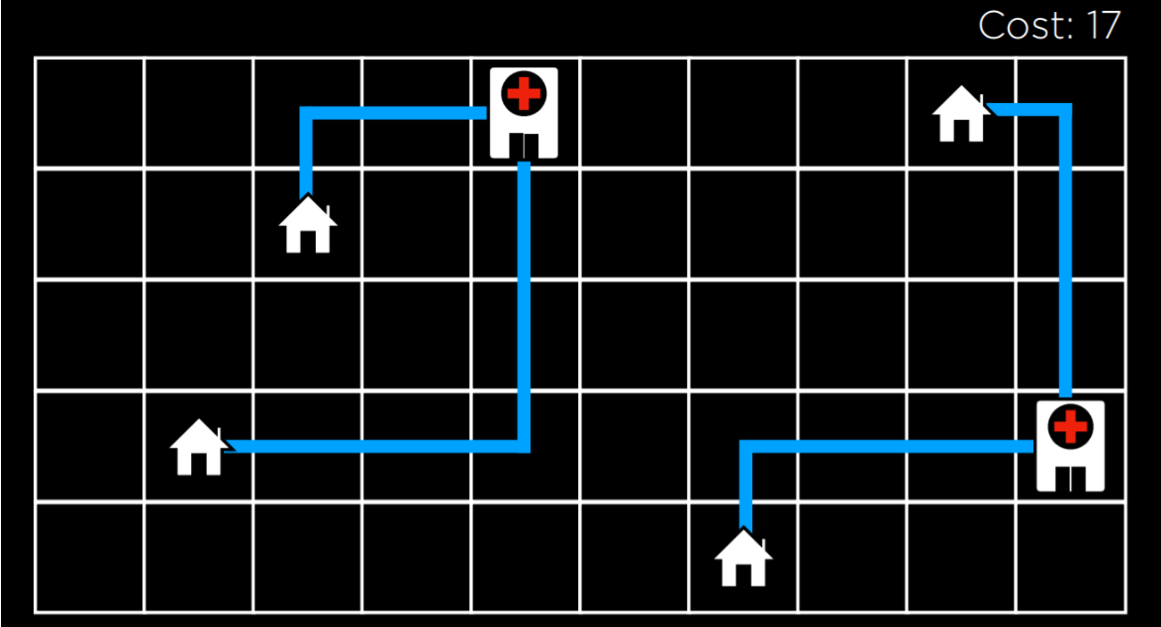
이 그림에서는 주택과 병원의 가능한 구성을 볼 수 있다. 이들 사이의 거리는 맨해튼 거리(위, 아래, 측면으로 이동한 횟수)를 사용하여 측정되며, 각 집에서 가장 가까운 병원까지의 거리의 합은 17(왼쪽:9, 오른쪽:8)이고, 우리는 이를 비용이라 부른다. 우리가 이 거리를 최소화하려고 노력하기 때문이다. 이 경우 state는 주택과 병원의 단일 구성이 된다.
이 개념을 추상화하면 주택과 병원의 각 구성을 아래의 상태공간 풍경으로 표현할 수 있다. 그림의 각 막대는 state의 가치를 나타내며, 이 예에서는 주택과 병원의 특정 구성에 대한 비용이 된다.
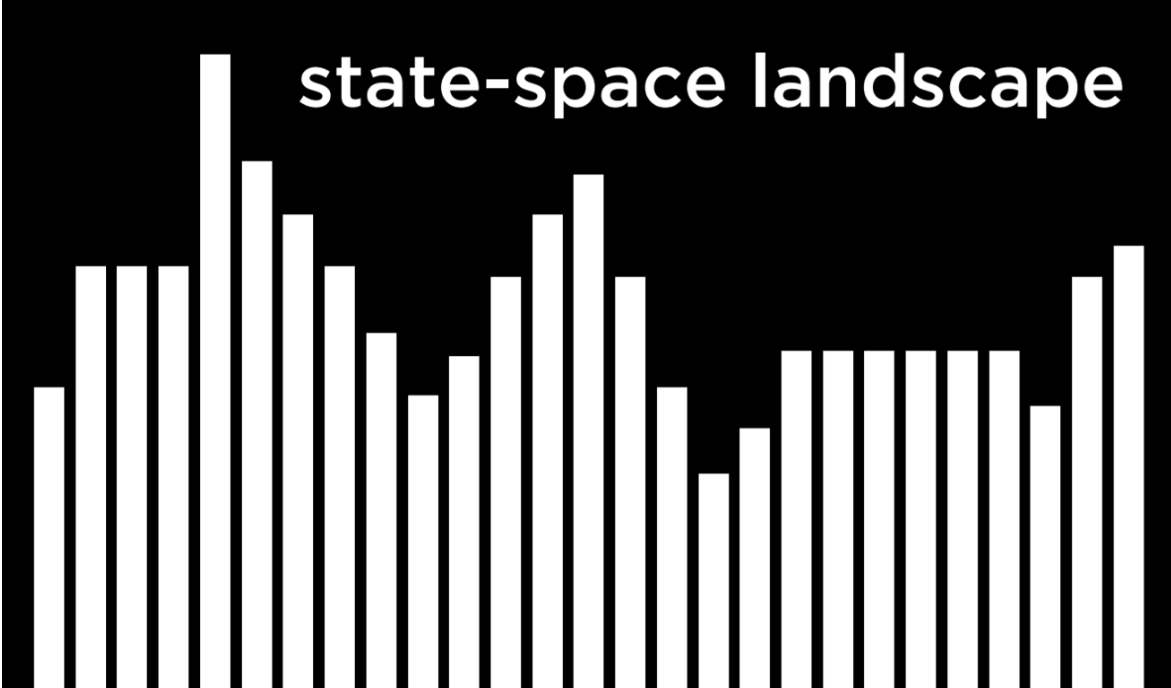
이 시각화를 벗어나서 나머지 문제를 위해 몇 가지 중요한 용어를 알아보자:
- 목적 함수: 솔루션의 가치를 최대화하는 데 사용하는 함수
- 비용 함수: 솔루션 비용을 최소화하기 위해 사용하는 함수(이는 주택과 병원의 예에서 사용할 함수이다. 우리는 집에서 병원까지의 거리를 최소화하려고 하기 때문)
- 현재 상태: 현재 함수에서 고려 중인 상태
- 이웃 상태: 현재 상태가 전환될 수 있는 상태. 위의 1차원 상태공간 환경에서 이웃 상태는 현재 상태의 양쪽에 있는 상태. 이 예에서 이웃 상태는 병원 중 하나를 임의의 방향으로 한 단계 이동한 결과로 발생하는 상태일 수 있다. 이웃 상태는 일반적으로 현재 상태와 유사하므로 해당 값은 현재 상태 값에 가깝다.
로컬 검색 알고리즘이 작동하는 방식은 현재 상태의 한 노드를 고려한 다음 해당 노드를 현재 상태의 이웃 중 하나로 이동하는 것이다. 이는 상태 공간의 모든 단일 상태를 재귀적으로 고려하는 미니맥스 알고리즘과 다르다.
언덕 오르기(Hill climb)
Hill climb은 지역 검색 알고리즘의 유형 중 하나이다. 이 알고리즘에서는 이웃 상태를 현재 상태와 비교하고, 그중 하나라도 더 나은 경우 현재 노드를 현재 상태에서 해당 이웃 상태로 변경한다. 더 나은 것의 자격은 더 높은 값을 선호하는 목적 함수를 사용하는지, 아니면 더 낮은 값을 선호하는 감소 함수를 사용하는지에 따라 정의된다.
언덕 오르기 알고리즘은 의사 코드에서 다음과 같다:
function Hill-Climb(problem):
- current = initial state of problem
- repeat:
- neighbor = best valued neighbor of current
- if neighbor not better than current:
- return current
- current = neighbor
이 알고리즘에서는 현재 상태(current = initial state of problem)부터 시작한다. 일부 문제에서는 현재 상태가 무엇인지 알 수 있지만, 다른 문제에서는 무작위로 하나를 선택하는 것부터 시작해야 한다.
- 그런 다음, 다음 작업을 반복한다.
- 이웃을 평가하여 가장 좋은 값을 가진 것을 선택한다(neighbor = best valued neighbor of current). 그런 다음, 이 이웃의 값을 현재 상태의 값과 비교한다.
- 이웃이 더 좋으면(current = neighbor), 현재 상태를 이웃 상태로 전환한 다음 프로세스를 반복한다.
- 가장 좋은 이웃을 현재 상태와 비교하면 프로세스가 종료되고 현재 상태가 더 좋아진다. 그런 다음 현재 상태를 반환한다.
언덕 오르기 알고리즘을 사용하여 예제에서 병원에 할당한 위치를 개선하기 위해 시작할 수 있다. 몇 번의 전환 후에는 다음과 같은 상태가 된다.
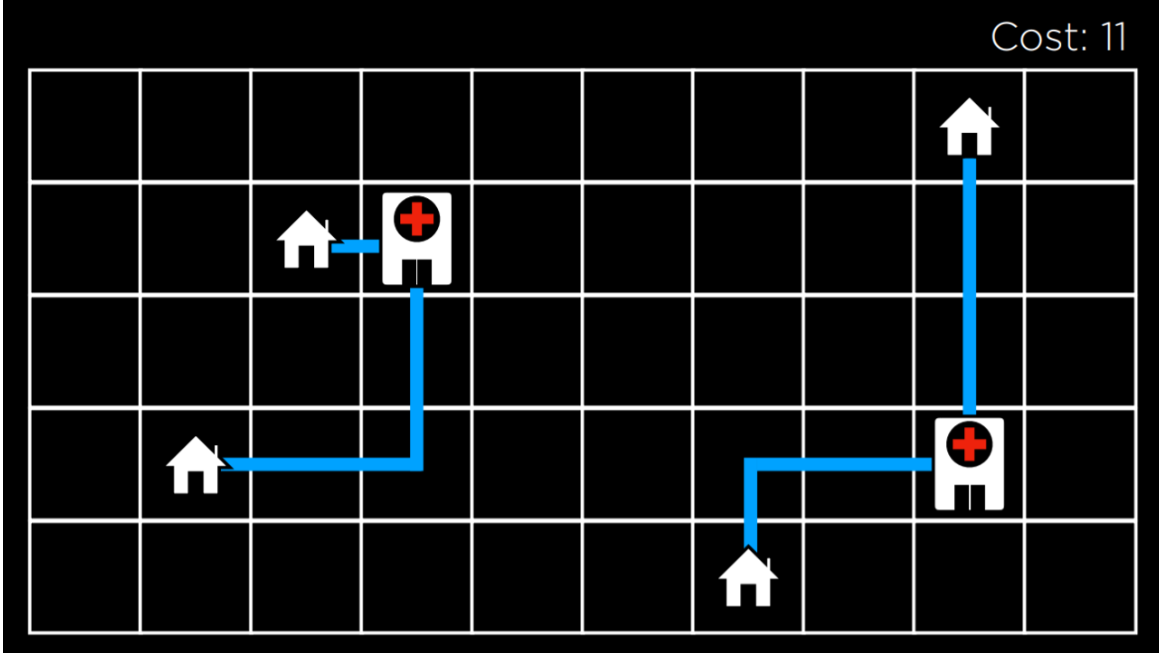
이 상태에서 비용은 11로, 이는 초기 상태의 비용인 17보다 향상되어 있다. 그러나 저 사진은 아직 최적의 상태는 아니다.
예를 들어 왼쪽에 있는 병원을 왼쪽 상단 집 아래로 이동하면 비용은 9가 되어 11보다 나아진다. 그러나 이 버전의 언덕 오르기 알고리즘은 거기에 도달할 수 없다. 왜냐하면 이웃 상태들이 적어도 현재 상태만큼 비용이 많이 들기 때문이다. 이러한 의미에서 언덕 오르기 알고리즘은 근시안적이며 종종 다른 것보다 더 나은 솔루션에 안주하지만 반드시 가능한 모든 솔루션 중 최고는 아니다.
극댓값과 극솟값
위에서 언급한 것처럼 언덕 오르기 알고리즘들은 극댓값들 또는 극솟값들에 갇힐 수 있다.
극댓값(local maximum (plural: maxima))은 이웃한 상태들보다 높은 값을 갖는 상태이고, 최댓값(global maximum)은 상태 공간의 모든 상태 중에서 가장 높은 값을 갖는 상태다.(고등수학 2 내용과 같다.)
// 참고로 영어에서는 maxima라고 해서 극댓값은 1개 이상이므로 복수형으로 사용하나 우리나라는 극댓값은 여러 개다라고 해서 따로 부르는 복수형은 없다.
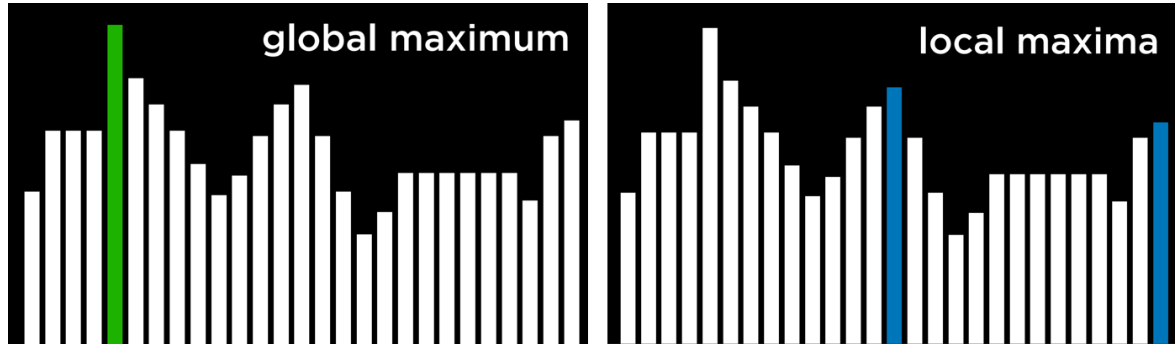
극솟값 local minimum(plural: minima)은
이웃한 상태들보다 낮은 값을 갖는 상태이고, 최솟값(global minimum)은 상태 공간의 모든 상태중에서 가장 닞은 값을 갖는 상태다.
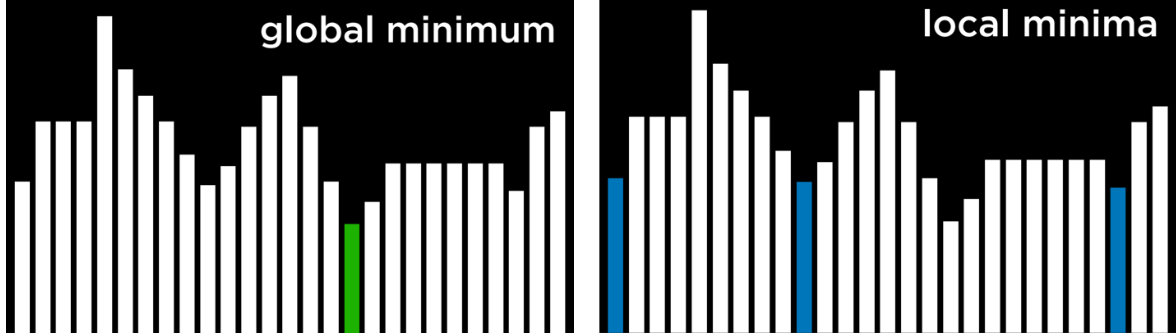
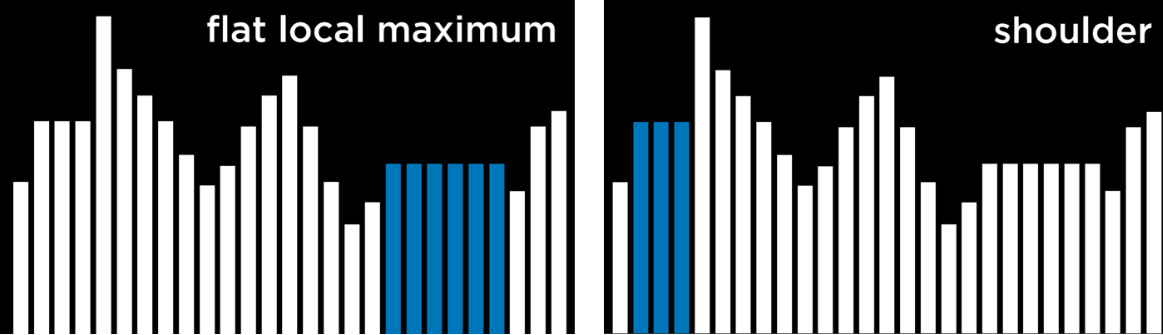
언덕 오르기 알고리즘의 문제점은 극댓값과 극솟값에 멈출 수 있다는 것이다. 알고리즘이 함수의 목적에 따라 현재 상태보다 더 나쁜 이웃이 있는 지점에 도달하면 알고리즘이 멈춘다. 극댓값과 극솟값의 특별한 유형인 편평한 극대값/극소값을 알아보자.
- 동일한 값의 여러 상태들이 인접하여 이웃이 더 나쁜 값을 갖는 편평한 고원이 있다.
- 동일한 값이 여러 상태들이 인접해 있고 고원의 이웃들이 더 좋을 수도 더 나쁠 수도 있는 숄더가 있다.
고원의 중간부터 시작한다면 알고리즘은 어떤 방향으로도 발전할 수 없다(히히 못가).
Hill Climbing 변형
Hill Climbing의 한계로 인해 극댓값과 극솟값에 갇히는 문제를 극복하기 위해 다양한 변형이 고려되었었다. 모든 변형된 알고리즘의 공통점은 전략에 관계없이 각 알고리즘은 여전히 극댓값과 극솟값으로 끝날 가능성이 있으며 최적화를 계속할 수단이 없다는 것이다. 아래 알고리즘은 값이 높을수록 좋다는 식으로 표현되어 있지만 비용을 최소화하는 것이 목표인 비용 함수에도 적용된다.
- Steepest-ascent : 가장 높은 가치를 지닌 이웃을 선택한다. 이것이 위에서 논의한 표준 변형이다.
- Stochastic(확률론적): 더 높은 가치의 이웃 중에서 무작위로 선택한다. 이를 통해 우리는 우리의 가치보다 더 나은 방향으로 나아가는 것을 선택한다. 예를 들어 가장 높은 값의 이웃이 극댓값으로 이어지는 반면 다른 이웃은 최대값으로 이어지는 경우 이는 의미가 있다.
- First-choice : 첫 번째로 높은 가치를 지닌 이웃을 선택한다.
- Random-restart: 언덕 등반을 여러 번 수행한다. 이때 매번 무작위 상태에서 시작한다. 그리고 모든 시행의 최대값을 비교하고 그중에서 가장 높은 것을 선택한다.
- Local Beam Search : 가장 높은 가치를 지닌 k 개의 이웃을 선택한다. 이는 검색에 하나가 아닌 여러 노드를 사용한다는 점에서 대부분의 로컬 검색 알고리즘과 다르다.
지역 검색 알고리즘이 항상 최상의 솔루션을 제공하는 것은 아니지만 가능한 모든 상태를 고려하는 것이 계산적으로 불가능한 상황에서는 종종 충분히 좋은 솔루션을 제공할 수 있게 된다.
Simulated Annealing(담금질 기법)
Hill climbing은 개선할 수 있는 변형을 해봤으나 모두 같은 결함을 가지고 있다. 아까 말했듯이 알고리즘이 극댓값에 도달하면 실행이 중지된다는 것이다. 담금질 기법을 통해 알고리즘은 극댓값에 갇힐 경우 자체적으로 "탈출"할 수 있다.
담금질은 금속을 가열하고 천천히 냉각시켜 금속을 단단하게 만드는 과정이다. 이는 높은 온도에서 시작해서 무작위 결정을 내릴 가능성이 높아지는 시뮬레이션된 어닐링 알고리즘에 대한 비유로 사용되며, 온도가 낮아질수록 무작위 결정을 내릴 가능성이 적어져 더욱 "확고"해진다. 이 메커니즘을 통해 알고리즘은 현재 상태보다 더 나쁜 이웃으로 상태를 변경할 수 있으며, 이는 로컬 최대값에서 벗어날 수 있는 방법이다. 다음은 담금질을 위한 의사코드이다:
function Simulated-Annealing(problem, max):
- current = initial state of problem
- for t = 1 to max:
- T = Temperature(t)
- neighbor = random neighbor of current
- ΔE = how much better neighbor is than current
- if ΔE > 0:
- current = neighbor
- with probability e^(ΔE/T) set current = neighbor
- return current
알고리즘은 문제와 반복해야 하는 횟수인 max를 입력으로 사용한다. 각 반복마다 T는 온도 함수를 사용하여 설정된다.
(온도 함수는 초기 반복( t 가 낮은 경우)에서 더 높은 값을 반환하고 이후 반복( t 가 높은 경우)에서는 더 낮은 값을 반환한다.)
- 그런 다음 무작위 이웃을 선택하고(neighbor = random neighbor of current), ΔE를 계산하여 현재 상태보다 이웃 상태가 얼마나 좋은지 정량화한다(ΔE = how much better neighbor is than current).
- 이전과 같이 이웃 상태가 현재 상태( ΔE > 0) 보다 좋으면 현재 상태를 이웃 상태로 설정한다.
- 그러나 이웃 상태가 더 나쁜 경우( ΔE < 0)에도(with probability e^(ΔE/T) set current = neighbor), 현재 상태를 해당 이웃 상태로 설정할 수 있으며 확률 e^( ΔE/T )로 그렇게 한다.
여기서 아이디어는 ΔE가 더 음수 일수록 이웃 상태가 선택될 확률이 낮아지고, 온도 T가 높을 수록 이웃 상태가 선택될 확률이 높아진다는 것이다. 즉, 이웃 상태가 나쁠수록 선택될 가능성이 낮아지고, 알고리즘 프로세스가 일찍 시작될수록 더 나쁜 이웃 상태를 현재 상태로 설정할 가능성이 높아진다.
이에 대한 계산은 다음과 같다. e는 상수(약 2.72)이고 ΔE 는 음수(이 이웃이 현재 상태보다 더 나쁨). ΔE가 음수일수록 결과 값은 0에 가까워진다. 온도 T가 높을수록 ΔE/T 는 0에 가까워지고 확률은 1에 가까워진다.
보부상 문제(Traveling Salesman Problem)
보부상 문제의 과제는 가능한 가장 짧은 거리를 선택하면서 모든 점을 연결하는 것이다. 예를 들어, 배송 회사가 해야 할 일은 매장에서 모든 고객의 집까지 왕복하는 최단 경로를 찾는 것이다.
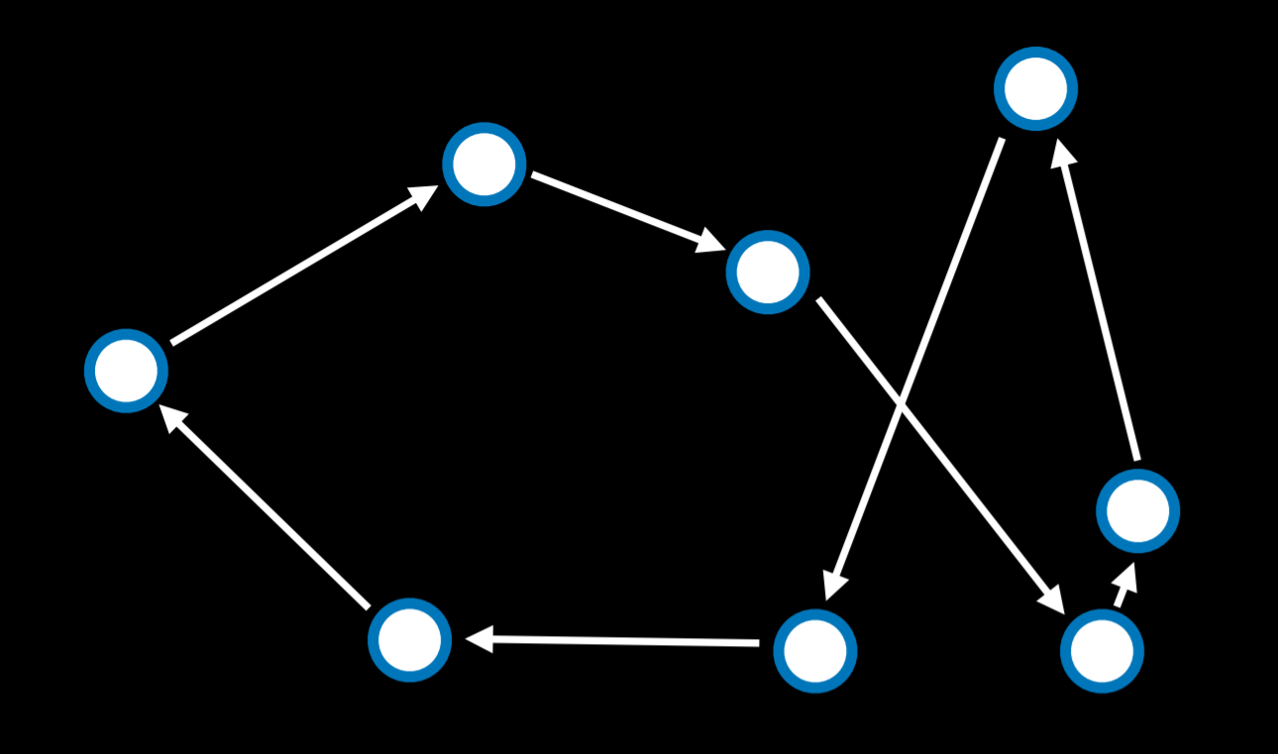
이 경우 이웃 상태는 두 개의 화살표가 위치를 바꾸는 상태로 볼 수 있다. 가능한 모든 조합을 계산하면 이 문제가 계산적으로 까다로워진(단지 10개의 포인트만 있으면 10! 또는 3,628,800개의 가능한 경로가 제공된다...).
담금 알고리즘을 사용하면 계산 비용을 낮추는 좋은 솔루션을 찾을 수 있다.
지금까지 최적화에서 지역탐색 파트를 알아봤다. 다음은 선형 프로그래밍 파트를 진행할 건데 수학 부분은 깊게 다루지는 않을 것이다.
'인공지능 > 인공지능개론' 카테고리의 다른 글
| [AI] Optimization (4-3) (1) | 2024.06.11 |
|---|---|
| [AI] Optimization (4-2) (0) | 2024.06.05 |
| [AI] Uncertainty(3-1) (0) | 2024.04.24 |
| [AI] Knowledge (2) (1) | 2024.04.20 |
| [AI] Search (1) (7) | 2024.04.11 |


