지식-기반 에이전트
지식 기반 에이전트
- 지식의 내적 표현에 의해 논증하는 에이전트를 지식 기반 에이전트라 한다.
- 지식을 바탕으로 논증해 결론을 도출한다라는 말이 뭔가?
ex) 오늘 비가 안왔으면, 해리는 해그리드에 갔다.
해리는 오늘 해그리드와 덤블도어 중 한 곳에만 갔다.
해리는 오늘 덤블도어에 갔다.
- 위의 세 문장으로 알 수 있는 것은 오늘 비가 왔는가? 에 대한 답이다. 논리적으로 덤블 도어에 갔으면 둘 중 한 곳만 갔으니 1번문장의 역을 도출 할 수 있다. 즉, 비가 왔으니 해그리드를 가지 않았다 = 비가 왔다
sentnece(문장): 문장은 지식 표현 언어로 된, 세계에 관한 주장이다. ai는 문장에 지식을 담아 새로운 정보를 추론한다.
Propositional Logic(명제 논리): 명제 논리는 명제에 기초한다. 명제란 세상에 대한 진술로, 참 또는 거짓이다.
명제 기호는 P, Q, R을 주로 사용한다.
- 논리 접속사는 세계에 대해 더 복잡한 방식으로 추론하기 위해 명제 기호를 연결하는 논리적 기호이다.
1. not( ¬P ): 진리 값 반전 = p는 참이다 -> ~p 는 거짓이다
2. and( P ∧ Q): P와 Q가 모두 참일 때만 ( P ∧ Q)가 참
3. or( P ∨ Q ): P와 Q가 모두 거짓일때만 ( P ∨ Q )가 거짓
4. 함축( (P → Q) )“P이면 Q이다”: P가 거짓이면 (P → Q) 는 항상 참이다, P가 참이면 (P → Q)은 Q의 진리값을 따른다.
5. 쌍조( P ↔ Q ): P → Q와 Q → P가 함께 이뤄지는 것과 같다. P와 Q의 진리값이 같으면 참 다르면 거짓이다.
Model(모델): 모델은 모든 명제에 대한 진리값의 할당이다.
ex){P= True, Q=False}같은 진리값 할당= 모델
- 명제가 2개가 있으면 모델은 4개가 셍긴다.(TT, TF, FT, FF)
지식 기반(KB): 지식 기반 에이전트가 아는 문장들의 집합이다. 이는 ai가 세계에 관해 명제 논리의 형채로 승인한 지식으로, 세계에 관한 추가적인 추론에 사용 가능하다.
Entailment(함의): α ⊨ β이면(α가 β를 함의하면), α가 참인 세계에서 β도 참이다. 함축과 다른용어이다.
함의는 α가 β의 정보를 포함하고 있는 관계이다.
Inference(추론): 추론은 기본 문장으로부터 새로운 문장을 도출하는 과정이다. 아까의 예시에서 비기 왔다, 해그리드를 가지 않았다의 문장들이 추론의 결과이다.

Inference Algorithms(추론 알고리즘)
모델 체킹 알고리즘
-KB ⊨ α인지 결정하려면(달리 말해, “우리의 지식 기반을 바탕으로 α가 참이라는 결론을 낼 수 있는가”라는 질문에 답하려면)
- 모든 가능한 모델을 열거한다.
- KB가 참인 모든 모델에서 α도 참이면, KB는 α를 함의한다(KB ⊨ α).
ex) P: 요일이다.
Q: 비가 내린다.
R: 해리는 달리기를 하러 갈 것이다.
KB: (P ∧ ¬Q) → R (말로 하자면, ‘P가 참이고 Q가 거짓’은 R을 함축한다) P (P가 참) ¬Q (Q는 거짓)
질의: R (우리는 R이 참인지 거짓인지 알고 싶다. KB ⊨ R인가?)

1. 모든 가능한 모델을 나열한다. = 진리표
2. 지식 기반에 대해 참인지 검사한다.
(P가 참이어야 하므로 P가 거짓이면 KB도 거짓, Q가 거짓이어야 하므로 Q가 참이면 KB는 거짓, R은 P가 참이고,Q가 거짓인 경우 R이 참이 되어야 한다.)
3. 우리가 알고 있는 조건(KB)를 다 사용하면 R이 참인 모델에서 KB가 참임을 알 수 있다.
함의의 정의에 따라 KB가 참인 모델에서 R이 참이면 KB ⊨ R이다.
Knowledge Engineering(지식 공학): AI에서 명제 논리를 어떻게 표현할지 알아내는 과정이다.
보드게임 클루를 예시를 들어 설명해보자:
우리는 모델체킹 알고리즘을 사용해 미스터리를 밝힌다. 우리의 모델에서는 살인자와 관련되었다고 아는 것을 True 로, 그렇지 않은 것을 False로 표시한다.
- 이 수업에서는 세 사람(머스타드, 플럼, 스칼렛), 세 가지 도구(칼, 권총, 렌치), 세 곳의 장소(무도회장, 주방, 도서관)가 있다고 가정한다.
- 먼저 게임 규칙을 추가해 지식 기반을 생성한다. 우리는 범인이 한 명이고, 범행에 도구가 한 개 사용됐고, 한 장소에서 벌어졌음을 안다. 이를 다음과 같은 명제 논리로 표현할 수 있다.
(Mustard ∨ Plum ∨ Scarlet)
(knife ∨ revolver ∨ wrench)
(ballroom ∨ kitchen ∨ library)
- 게임은 각 플레이어가 한 사람, 하나의 도구, 하나의 장소를 보고 살인과 관련이 없음을 아는 것으로 시작된다. 플레이어는 이 카드에서 본 정보를 공유하지 않는다. 플레이어가 머스타드, 주방, 리볼버 카드를 받았다고 가정해 보자. 따라서 우리는 이것이 살인과 관련이 없다는 것을 알고 있으며 KB에 추가할 수 있다.
¬(Mustard)
¬(kitchen)
¬(revolver)
- 게임의 다른 상황에서는 사람, 도구, 위치의 조합을 제안하여 추측할 수 있다. 스칼렛이 도서관에서 범죄를 저지르기 위해 렌치를 사용했다고 추측한다고 가정해 보자. 이 추측이 틀리면 다음을 추론하여 KB에 추가할 수 있다.
(¬Scarlet ∨ ¬library ∨ ¬렌치)
- 이제 누군가가 우리에게 Plum 카드를 보여줬다고 가정해 보자. 따라서 우리는 다음을 추가할 수 있다.
¬(Plum)
- 이 시점에서 우리는 살인자가 Scarlet이라고 결론을 내릴 수 있다. 머스타드, 플럼, 스칼렛 중 하나여야 하고, 처음 두 사람은 그렇지 않다는 증거가 있기 때문이다.
- 예를 들어, 무도회장이 아니라는 지식을 하나만 더 추가하면 더 많은 정보를 얻을 수 있다. 먼저 KB를 업데이힌다.
¬(연회장)
이제 이전의 여러 데이터를 사용하여 스칼렛이 도서관에서 칼로 살인을 저질렀다는 것을 추론할 수 있다.
논리퍼즐, Mastermind 게임도 있는데 안나올 거 같으니 넘기겠다.
Inference Rules(추론 규칙)
모델 검사는 답변을 제공하기 전에 가능한 모든 모델을 고려해야 하기 때문에 효율적인 알고리이 아니다(알림: KB가 참인 모든 모델(진리 할당)에서 R도 참인 경우 쿼리 R은 참임). 추론 규칙을 사용하면 가능한 모든 모델을 고려하지 않고 기존 지식을 기반으로 새로운 정보를 생성할 수 있다.
추론 규칙은 일반적으로 상단 부분인 전제와 하단 부분인 결론을 구분하는 가로선을 사용하여 표현된다.
전제: 우리가 가지고 있는 모든 지식이고
결론: 전제를 기반으로 지식이 생성될 수 있다는 것이다.
이 예에서 우리의 전제는 다음 명제로 구성된다.
- 비가 오면 해리가 안에 있다.
- 비가 온다.
이를 바탕으로 가장 합리적인 인간은 다음과 같이 결론을 내릴 수 있다.
- 해리가 안에 있다.
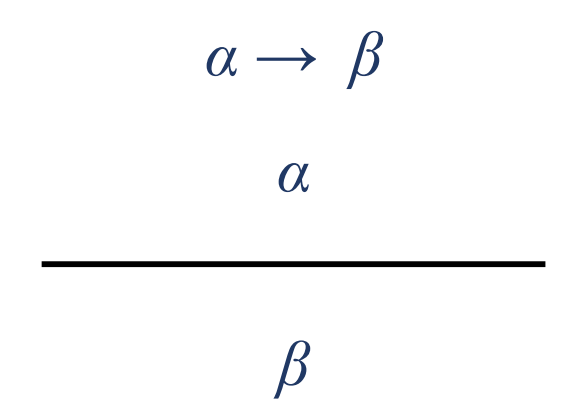
긍정 논법: 함축과 전제가 참이면 결론도 참이다.

논리곱 소거: And 명제가 참이면 알파 베타가 참이다.
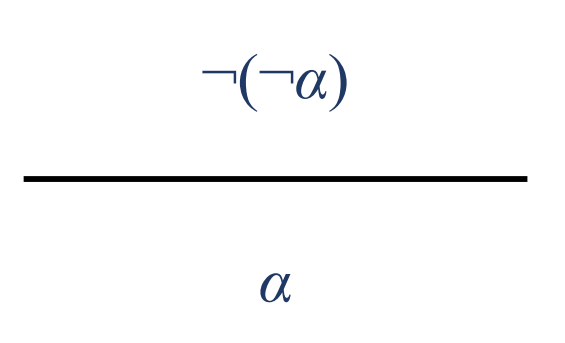
이중 부정 소거: 두번 부정된 명제는 참이다.

함축 제거: 위 아래 두개의 진리값은 같다.

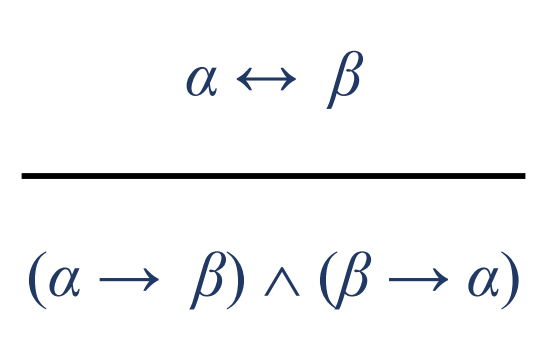
쌍 조건문 소거: 쌍 조건 명제는 함축과 그것의 역을 and한 것과 동치이다.
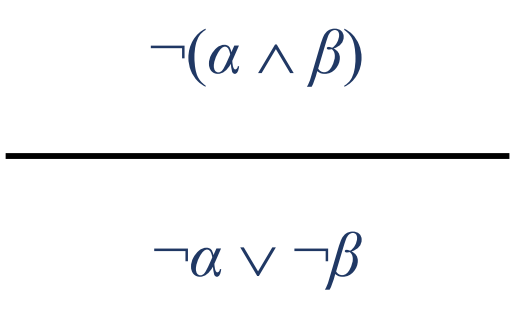
드모르간 법칙: 위 아래가 같다.


분배 법칙: 괄호 안에 있으면 분배 법칙이 가능하다.
Search Problems(탐색 문제): 추론을 다음 속성을 지닌 탐색 문제로 볼 수 있다.
- 초기 상태: 지식 기반을 시작
- 행동: 추론 규칙
- 전이 모델: 추론 이후의 새로운 지식 기반
- 목표 테스트: 우리가 증명하려는 진술이 지식 기반에 있는지 확인
- 경로비용 함수: 증명의 단계 수
이것은 우리가 추론 규칙을 사용하여 기존 지식을 기반으로 새로운 정보를 도출할 수 있도록 하는 검색 알고리듬이 얼마나 다양한지 보여준다.
Resolution(분해)
-분해는 Or 명제의 두 원자 명제 중 하나가 거짓이면 다른 하나는 참이어야 한다는 강력한 추론 규칙이다.

분해는 P 및 ¬P와 같이 하나는 부정되고 다른 하나는 그렇지 않은 동일한 원자 명제 중 두 가지인 보수 리터럴(Complementary Literal)에 의존한다.
즉, (P ,~P)가 보수 리터럴이다.

분해를 더 일반화할 수 있다. "론이 그레이트 홀에 있다" 또는 "헤르미온느가 도서관에 있다"라는 명제 외에 "론이 그레이트 홀에 없다" 또는 "해리가 자고 있다"라는 명제도 알고 있다고 가정한다. 우리는 이것으로부터 "헤르미온느가 도서관에 있다" 또는 "해리가 자고 있다"라고 분해를 사용하여 추론할 수 있다. 공식 용어로 표현하자면 다음과 같다.
보수 리터럴을 사용하면 해결에 의한 추론을 통해 새로운 문장을 생성할 수 있다. 따라서 추론 알고리듬은 보수 리터럴을 찾아 새로운 지식을 생성한다.
논리곱 정규형:
- 절은 리터럴(명제 기호 또는 명제 기호의 부정, 예를 들어 P, ¬P)들의 선언이다.
- 선언은 Or 논리 접속사로 연결된 명제들로 구성된다(P ∨ Q ∨ R).
- 한편, 연언은 And 논리 접속사로 연결된 명제들로 구성된다(P ∧ Q ∧ R).
- 논리문을 절들의 연언인 논리곱 정규형으로 변환할 수 있다. 예: (A ∨ B ∨ C) ∧ (D ∨ ¬E) ∧ (F ∨ G)
명제를 논리곱 정규형으로 변환하는 순서는 다음과 같다.
- 쌍조건문을 소거
- (α ↔ β)를 (α → β) ∧ (β → α)로 바꾼다.
- 함축을 제거
- (α → β)를 ¬α ∨ β로 바꾼다.
- De Morgan의 법칙을 사용하여 리터럴만 부정될 때까지(절이 아니라) 부정을 안쪽으로 이동한다.
- ¬(α ∧ β)를 ¬α ∨ ¬β로 바꾼다.
(P ∨ Q) → R을 논리곱 정규형으로 변환한 예는 다음과 같다.
- (P ∨ Q) → R
- ¬(P ∨ Q) ∨ R /함축을 제거
- (¬P ∧ ¬Q) ∨ R /드 모르강 법칙(De Morgan's Law)
- (¬P ∨ R) ∧ (¬Q ∨ R) /분배 법칙(Distributive Law)
이 시점에서 결합 정규형에 대한 추론 알고리즘을 실행할 수 있다. 때로는 분해에 의한 추론 과정을 통해 절에 동일한 리터럴이 두 번 포함되는 경우가 발생할 수 있다. 이러한 경우 중복 리터럴이 제거되는 factoring 프로세스가 사용된다. 예를 들어, (P ∨ Q ∨ S) ∧ (¬P ∨ R ∨ S)를 통해 (Q ∨ S ∨ R ∨ S)를 분해로 추론할 수 있다. 중복된 S를 제거하여 (Q ∨ R ∨ S)를 얻을 수 있다
모순:
리터럴과 그 부정(예: ¬P 및 P)을 분해하면 빈 절()이 된다. 빈 절은 항상 거짓이며, P와 ¬P가 모두 참일 수 없기 때문에 이는 의미가 있다. 이 사실은 분해 알고리즘에 사용된다.
- KB ⊨ α인지 결정:
- 확인: (KB ∧ ¬α)는 모순인가?
- 그렇다면 KB ⊨ α다.
- 그렇지 않다면 함축이 아니다.
- 확인: (KB ∧ ¬α)는 모순인가?
분해를 통한 추론:
모순에 의한 증명은 컴퓨터 과학에서 자주 사용되는 도구이다. 우리의 지식 기반(KB)이 참이고 ¬α와 모순되는 경우, 이는 ¬α가 거짓이고 따라서 α가 참이어야 함을 의미한다. 보다 기술적으로 알고리즘은 다음 작업을 수행한다.
- KB ⊨ α인지 확인하려면:
- (KB ∧ ¬α)를 논리곱 정규형으로 변환한다.
- 분해를 통해 새 절을 생성할 수 있는지 계속 확인한다.
- 빈 절(False에 해당)이 생성되면 축하한다! 우리는 모순에 도달하여 KB ⊨ α임을 증명한다.
- 그러나 모순이 성립되지 않고 더 이상 절을 유추할 수 없으면 함의가 없다.
다음은 이 알고리즘이 작동하는 방식을 보여주는 예이다.
- (A ∨ B) ∧ (¬B ∨ C) ∧ (¬C)는 A를 함의하는가?
- 첫째, 모순으로 증명하기 위해 우리는 A가 거짓이라고 가정한다. 따라서 우리는 (A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)에 도달한다. (KB: (A ∨ B) (¬B ∨ C) (¬C) (¬A) )
- 이제 새로운 정보 생성을 시작할 수 있다. 우리는 C가 거짓(¬C)이라는 것을 알고 있기 때문에 B가 거짓인 경우에만(¬B ∨ C) 참 이 될 수 있다. 따라서 KB에 (¬B)를 추가할 수 있다. (KB: (A ∨ B) (¬B ∨ C) (¬C) (¬A) + (¬B) )
- 다음으로, 우리는 (¬B)를 알고 있으므로 (A ∨ B)가 참일 수 있는 유일한 방법은 A가 참일 때뿐이다. 따라서 KB에 (A)를 추가할 수 있다. (KB: (A ∨ B) (¬B ∨ C) (¬C) (¬A) (¬B) + (A) )
- 이제 KB에는 두 개의 보수 리터럴, (A) 및 (¬A)가 있다. 우리는 그것들을 해결하고 빈 집합()에 도달한다. 빈 집합은 정의상 거짓이므로 모순에 도달했다. (KB: (A ∨ B) (¬B ∨ C) (¬C) (¬A) (¬B) (A) + () )
일차 논리
- 일차 논리는 명제 논리보다 복잡한 개념을 간명하게 표현할 수 있다. 일차 논리에서는 상수 기호와 술어 기호를 사용한다. - 상수 기호: 개체를 나타낸다.
- 술어 기호: 관계, 혹은 인자를 취해 참 또는 거짓 값을 반환하는 함수와 비슷하다.
예시)
이번에는 사람과 집을 다르게 할당하겠다.
상수 기호는 미네르바, 포모나, 그리핀도르, 후플푸프 등과 같은 사람이나 집이다.
술어 기호는 일부 상수 기호의 참 또는 거짓을 갖는 속성이다.
예를 들어,
Person(Minerva)라는 문장을 사용하여 미네르바가 사람이라는 개념을 표현할 수 있다.
House(Gryffindor)라는 문장을 사용하여 그리핀도르가 집이라는 개념을 표현할 수 있다.
모든 논리적 연결은 이전과 동일한 방식으로 일차 논리에서 작동한다.
예를 들어 ¬House(Minerva)는 미네르바가 집이 아니라는 개념을 표현한다.
술어 기호는 두 개 이상의 인수를 취하고 이들 간의 관계를 표현할 수도 있다. 예를 들어 BelongsTo는 사람과 그 사람이 속한 집이라는 두 인수 간의 관계를 나타낸다.
따라서 미네르바가 그리핀도르에 속한다는 개념을 BelongsTo(Minerva, Gryffindor)로 표현할 수 있다.
일차 논리는 각 사람에 대해 하나의 기호와 각 집에 대해 하나의 기호를 가질 수 있다. 이것은 각 사람—집 할당이 다른 기호를 요구하는 명제 논리보다 더 간결하다.
보편 양화:
- 양화는 특정 상수 기호를 사용하지 않고 문장을 표현하기 위해 일차 논리에서 사용할 수 있는 도구이다.
- 보편 양화는 ∀ 기호를 사용하여 “모두에 대해”를 표현한다.
- 모든 x에 대해 참인 문장을 만든다.
예를 들어, 문장 ∀x. BelongsTo(x, Gryffindor) → ¬BelongsTo(x, Hufflepuff)는 이 기호가 그리핀도르에 속하면 후플푸프에 속하지 않는다는 것이 모든 기호에 대해 참이라는 개념을 표현한다.
존재 양화: 보편 양화와 유사한 개념이다.
-적어도 하나의 x에 대해 참인 문장을 만드는 데 사용된다. ∃ 기호로 표현한다.
예를 들어, 문장 ∃x. House(x) ∧ BelongsTo(Minerva, x)는 집이면서 미네르바가 속한 심볼이 하나 이상 있음을 의미한다. 즉, 이것은 미네르바가 집에 속해 있다는 개념을 표현한 것이다.
존재 양화와 보편 양화는 같은 문장에서 사용될 수 있다. 예를 들어 문장 ∀x. Person(x) → (∃y. House(y) ∧ BelongsTo(x, y))는 x가 사람이면 이 사람이 속한 적어도 하나의 집 y가 있다는 개념을 표현한다. 즉, 이 문장은 모든 사람이 집에 속해 있다는 의미이다.
다른 유형의 논리도 있으며 이들의 공통점은 모두 정보를 표현하기 위해 존재한다는 것이다. 이것은 우리가 AI에서 지식을 표현하는 데 사용하는 체계이다.
'인공지능 > 인공지능개론' 카테고리의 다른 글
| [AI] Optimization (4-3) (1) | 2024.06.11 |
|---|---|
| [AI] Optimization (4-2) (0) | 2024.06.05 |
| [AI] Optimization (4-1) (1) | 2024.06.05 |
| [AI] Uncertainty(3-1) (0) | 2024.04.24 |
| [AI] Search (1) (7) | 2024.04.11 |


