#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// ===== 원형큐 코드 시작 ======
#define MAX_QUEUE_SIZE 5
typedef int element;
typedef struct { // 큐 타입
element data[MAX_QUEUE_SIZE];
int front, rear;
} QueueType;
// 오류 함수
void error(char *message)
{
fprintf(stderr, "%s\n", message);
exit(1);
}
// 공백 상태 검출 함수
void init_queue(QueueType *q)
{
q->front = q->rear = 0;
}
// 공백 상태 검출 함수
int is_empty(QueueType *q)
{
return (q->front == q->rear);
}
// 포화 상태 검출 함수
int is_full(QueueType *q)
{
return ((q->rear + 1) % MAX_QUEUE_SIZE == q->front);
}
// 원형큐 출력 함수
void queue_print(QueueType *q)
{
printf("QUEUE(front=%d rear=%d) = ", q->front, q->rear);
if (!is_empty(q)) {
int i = q->front;
do {
i = (i + 1) % (MAX_QUEUE_SIZE);
printf("%d | ", q->data[i]);
if (i == q->rear)
break;
} while (i != q->front);
}
printf("\n");
}
// 삽입 함수
void enqueue(QueueType *q, element item)
{
if (is_full(q))
error("큐가 포화상태입니다");
q->rear = (q->rear + 1) % MAX_QUEUE_SIZE;
q->data[q->rear] = item;
}
// 삭제 함수
element dequeue(QueueType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다");
q->front = (q->front + 1) % MAX_QUEUE_SIZE;
return q->data[q->front];
}
// 삭제 함수
element peek(QueueType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다");
return q->data[(q->front + 1) % MAX_QUEUE_SIZE];
}
// ===== 원형큐 코드 끝 ======
int main(void)
{
QueueType queue;
int element;
init_queue(&queue);
printf("--데이터 추가 단계--\n");
while (!is_full(&queue))
{
printf("정수를 입력하시오: ");
scanf("%d", &element);
enqueue(&queue, element);
queue_print(&queue);
}
printf("큐는 포화상태입니다.\n\n");
printf("--데이터 삭제 단계--\n");
while (!is_empty(&queue))
{
element = dequeue(&queue);
printf("꺼내진 정수: %d \n", element);
queue_print(&queue);
}
printf("큐는 공백상태입니다.\n");
return 0;
}CH.1
중요도 ★
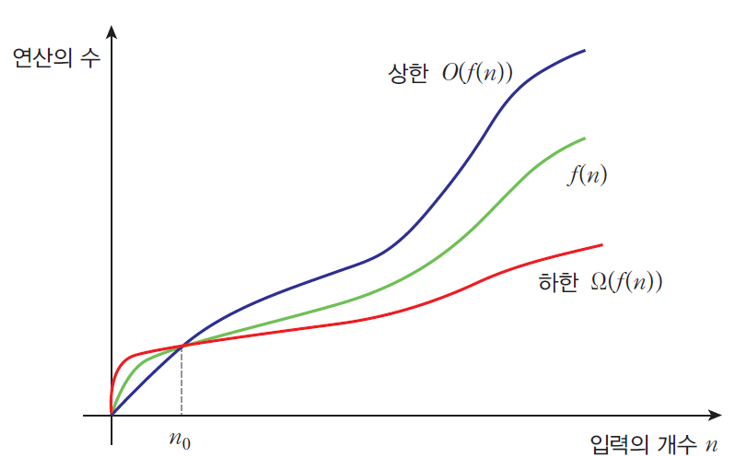
빅오 표기법: 연산 횟수를 대략적으로 표기한 것
모든 n≥n0에 대하여 |f(n)| ≤ c|g(n)| 을 만족하는 2개의 상수 c와 n0가 존재하면 f(n)=O(g(n))이다.

빅오메가 표기법
빅세타 표기법(밑줄 쫙)
코드: factorial.c (순환)
factorial(3);
f3
ㄴf2 x 3
ㄴ f1 x 2
ㄴf1=1
차례로 진행되고 값을 반대로 리턴
etc) ppt 2. slide 6
디버깅은 진행과정을 이해하는 과정이다.(엄근진)
stack: 임시공간
함수의 파라미터가 해당 함수의 스택에 저장됨 ex)파라미터= factorial(3) stack= 메모리안에 있는 factorial3
아래에서부터 메모리를 할당함(스택이 쌓임) -> 함수가 끝이 나면 메모리 반환(중괄호를 만나거나 return을 만날 때)
메모리가 반환이 되면 그안에 값을 리턴함 -> 그 후 메모리 삭제됨 = 운영체제로 반납됨
-------------------------------
코드:factorial_iter (반복)
for문을 사용하여 간단하게 해결
스택 사용 안함(간단한 경우)
스택 사용하는 경우도 있음(프로그래머가 직접 만들어서) = 스택 프로그래밍
-----------------------------------------------
거듭제곱(순환,반복 가능)
이상함: 반복에서 오버헤드 많이 일어남/ 순환에선 별루 안남
why?
반복문: x를 n번 곱한다.
순환문: 짝수 홀수 나눠서
코드: power.c (순환) ★ ★ ★
input의 값이 절반씩 줄어든다.
지수적으로 감소한다 = 로그함수
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
double power(double x, int n) //순환
{
if( n==0 ) return 1;
else if ( (n%2)==0 )
return power(x*x, n/2);
else return x*power(x*x, (n-1)/2);
}
int main() {
int val;
val = power(3, 3);
printf("power(x,n): %d\n", val);
}
slow_power.c (반복)
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
double slow_power(double x, int n) //반복
{
int i;
double result = 1.0;
for (i = 0; i<n; i++)
result = result * x;
return(result);
}
int main() {
int val;
val = slow_power(2,3);
printf("slow_power(x,n): %d\n", val);
}
CH.3
중요도 ★ ★ ★ ★ ★(숙제)
배열: 배열 인덱스/ 같은 데이터를 모아놓음
adt: 배열은 객체다. <인덱스, 값>의 집합
create: size개의 요소를 생성
get(a,i):a의 i번째 요소 반환
size(a,i,v): a의 i번째 위치에 v저장
1차원
2차원
구조체: 타입이 다른 데이터를 묶음
ex)학생, 나이, 성적 등
코드: structure
구조체 값
------------------------
배열의 응용: 다항식
차수에 대한 계수를 하나씩 넣을 수 있음 그렇게 하나의 배열 완성
★ ★ ★ ★ ★
행렬: matrix 2차원 배열을 사용하여 배열전체를 저장
하드코딩도 해보기
코드 준거: 2차원배열써야되는지랑 기타등등 뜯고맛보기
포인터: 스왑이랑 배열을 같이 쓰는 코드
//hard-coding 버전
#include <iostream>
using namespace std;
int main()
{
int sparseMatrix[4][5] =
{
{0 , 0 , 3 , 0 , 4 },
{0 , 0 , 5 , 7 , 0 },
{0 , 0 , 0 , 0 , 0 },
{0 , 2 , 6 , 0 , 0 }
};
int size = 0;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 5; j++)
if (sparseMatrix[i][j] != 0)
size++;
int compactMatrix[6][3];
// Making of new matrix
int k = 0;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 5; j++)
if (sparseMatrix[i][j] != 0)
{
compactMatrix[k][0] = i;
compactMatrix[k][1] = j;
compactMatrix[k][2] = sparseMatrix[i][j];
k++;
}
for (int i = 0; i < size; i++)
{
for (int j = 0; j < 3; j++)
cout << " " << compactMatrix[i][j];
cout << "\n";
}
return 0;
}
다 아는 스왑 ★★★
#include <stdio.h>
void swap(int *px, int *py)
{
int tmp;
tmp = *px;
*px = *py;
*py = tmp;
}
int main(void)
{
int a = 1, b = 2;
printf("swap을 호출하기 전: a=%d, b=%d\n", a, b);
swap(&a, &b);
printf("swap을 호출한 다음: a=%d, b=%d\n", a, b);
return 0;
}
CH.4
stack ★★★ ★★★ ★★★ ★★★
스택단점:정적(정해짐)
그럼 동적 만들면 그만이야~=malloc()
응용:스택으로 괄호가 맞는지 활용가능
-->스택을 이용해서 컴파일러가 문법체크해줌
infix.c 중위표기식 -> 후위표기식
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_STACK_SIZE 100
typedef char element; // 교체!
// 차후에 스택이 필요하면 여기만 복사하여 붙인다.
// ===== 스택 코드의 시작 =====
#define MAX_STACK_SIZE 100
typedef struct {
element data[MAX_STACK_SIZE];
int top;
} StackType;
// 스택 초기화 함수
void init_stack(StackType *s)
{
s->top = -1;
}
// 공백 상태 검출 함수
int is_empty(StackType *s)
{
return (s->top == -1);
}
// 포화 상태 검출 함수
int is_full(StackType *s)
{
return (s->top == (MAX_STACK_SIZE - 1));
}
// 삽입함수
void push(StackType *s, element item)
{
if (is_full(s)) {
fprintf(stderr, "스택 포화 에러\n");
return;
}
else s->data[++(s->top)] = item;
}
// 삭제함수
element pop(StackType *s)
{
if (is_empty(s)) {
fprintf(stderr, "스택 공백 에러\n");
exit(1);
}
else return s->data[(s->top)--];
}
// 피크함수
element peek(StackType *s)
{
if (is_empty(s)) {
fprintf(stderr, "스택 공백 에러\n");
exit(1);
}
else return s->data[s->top];
}
// ===== 스택 코드의 끝 =====
// 연산자의 우선순위를 반환한다.
int prec(char op)
{
switch (op) {
case '(': case ')': return 0;
case '+': case '-': return 1;
case '*': case '/': return 2;
}
return -1;
}
// 중위 표기 수식 -> 후위 표기 수식
void infix_to_postfix(char exp[])
{
int i = 0;
char ch, top_op;
int len = strlen(exp);
StackType s;
init_stack(&s); // 스택 초기화
for (i = 0; i<len; i++) {
ch = exp[i];
switch (ch) {
case '+': case '-': case '*': case '/': // 연산자
// 스택에 있는 연산자의 우선순위가 더 크거나 같으면 출력
while (!is_empty(&s) && (prec(ch) <= prec(peek(&s))))
printf("%c", pop(&s));
push(&s, ch);
break;
case '(': // 왼쪽 괄호
push(&s, ch);
break;
case ')': // 오른쪽 괄호
top_op = pop(&s);
// 왼쪽 괄호를 만날때까지 출력
while (top_op != '(') {
printf("%c", top_op);
top_op = pop(&s);
}
break;
default: // 피연산자
printf("%c", ch);
break;
}
}
while (!is_empty(&s)) // 스택에 저장된 연산자들 출력
printf("%c", pop(&s));
}
//
int main(void)
{
char *s = "(2+3)*4+9*2";
printf("중위표시수식 %s \n", s);
printf("후위표시수식 ");
infix_to_postfix(s);
printf("\n");
return 0;
}
->연산자만 스택에 저장했다가 출력하면 된다.
---------------------------------------
CH.5
큐: 삽입, 삭제/ 선입선출
선형큐: -로 초기화 why? 배열이니까~ +주둥이가 2개다(rear, front)
인덱스 0부터 시작 그래서 rear 1증가시키고 삽입,
삭제도 마찬가지로 front 1 증가시키고 그 위치삭제(ppt 6슬라이드)
포인터 사용 이유
이유 추정: 함수 호출이 문제다
call by value/ call by address -c언어
지역변수라 함수 안에서만 작동됨 따라서 함수 호출을 하려면 포인터로 직접 가리켜야 함수가 나올때 값을 갖고 있을 수 있다.
선형큐의 문제점: 뒤가 가득 차버리면 앞이 비어도 쓸 수 없음 /증가만 하기 때문
rear가 앞에것을 사용하기 위해 뒤를 앞에다가 연결해버림
그것이 원형큐다
원형큐: 초기값=0
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// ===== 원형큐 코드 시작 ======
#define MAX_QUEUE_SIZE 5
typedef int element;
typedef struct { // 큐 타입
element data[MAX_QUEUE_SIZE];
int front, rear;
} QueueType;
// 오류 함수
void error(char *message)
{
fprintf(stderr, "%s\n", message);
exit(1);
}
// 공백 상태 검출 함수
void init_queue(QueueType *q)
{
q->front = q->rear = 0;
}
// 공백 상태 검출 함수
int is_empty(QueueType *q)
{
return (q->front == q->rear);
}
// 포화 상태 검출 함수
int is_full(QueueType *q)
{
return ((q->rear + 1) % MAX_QUEUE_SIZE == q->front);
}
// 원형큐 출력 함수
void queue_print(QueueType *q)
{
printf("QUEUE(front=%d rear=%d) = ", q->front, q->rear);
if (!is_empty(q)) {
int i = q->front;
do {
i = (i + 1) % (MAX_QUEUE_SIZE);
printf("%d | ", q->data[i]);
if (i == q->rear)
break;
} while (i != q->front);
}
printf("\n");
}
// 삽입 함수
void enqueue(QueueType *q, element item)
{
if (is_full(q))
error("큐가 포화상태입니다");
q->rear = (q->rear + 1) % MAX_QUEUE_SIZE;
q->data[q->rear] = item;
}
// 삭제 함수
element dequeue(QueueType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다");
q->front = (q->front + 1) % MAX_QUEUE_SIZE;
return q->data[q->front];
}
// 삭제 함수
element peek(QueueType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다");
return q->data[(q->front + 1) % MAX_QUEUE_SIZE];
}
// ===== 원형큐 코드 끝 ======
int main(void)
{
QueueType queue;
int element;
init_queue(&queue);
printf("--데이터 추가 단계--\n");
while (!is_full(&queue))
{
printf("정수를 입력하시오: ");
scanf("%d", &element);
enqueue(&queue, element);
queue_print(&queue);
}
printf("큐는 포화상태입니다.\n\n");
printf("--데이터 삭제 단계--\n");
while (!is_empty(&queue))
{
element = dequeue(&queue);
printf("꺼내진 정수: %d \n", element);
queue_print(&queue);
}
printf("큐는 공백상태입니다.\n");
return 0;
}
-------------
덱(deque): 앞뒤로 삽입과 삭제가 가능함
큐 (시계 방향)와 다르게 반시계 방향으로 회전 필요
#include <stdio.h>
#include <stdlib.h>
#define MAX_QUEUE_SIZE 5
typedef int element;
typedef struct { // 큐 타입
element data[MAX_QUEUE_SIZE];
int front, rear;
} DequeType;
// 오류 함수
void error(char *message)
{
fprintf(stderr, "%s\n", message);
exit(1);
}
// 초기화
void init_deque(DequeType *q)
{
q->front = q->rear = 0;
}
// 공백 상태 검출 함수
int is_empty(DequeType *q)
{
return (q->front == q->rear);
}
// 포화 상태 검출 함수
int is_full(DequeType *q)
{
return ((q->rear + 1) % MAX_QUEUE_SIZE == q->front);
}
// 원형큐 출력 함수
void deque_print(DequeType *q)
{
printf("DEQUE(front=%d rear=%d) = ", q->front, q->rear);
if (!is_empty(q)) {
int i = q->front;
do {
i = (i + 1) % (MAX_QUEUE_SIZE);
printf("%d | ", q->data[i]);
if (i == q->rear)
break;
} while (i != q->front);
}
printf("\n");
}
// 삽입 함수
void add_rear(DequeType *q, element item)
{
if (is_full(q))
error("큐가 포화상태입니다");
q->rear = (q->rear + 1) % MAX_QUEUE_SIZE;
q->data[q->rear] = item;
}
// 삭제 함수
element delete_front(DequeType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다");
q->front = (q->front + 1) % MAX_QUEUE_SIZE;
return q->data[q->front];
}
// 삭제 함수
element get_front(DequeType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다");
return q->data[(q->front + 1) % MAX_QUEUE_SIZE];
}
void add_front(DequeType *q, element val)
{
if (is_full(q))
error("큐가 포화상태입니다");
q->data[q->front] = val;
q->front = (q->front - 1 + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
}
element delete_rear(DequeType *q)
{
int prev = q->rear;
if (is_empty(q))
error("큐가 공백상태입니다");
q->rear = (q->rear - 1 + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
return q->data[prev];
}
element get_rear(DequeType *q)
{
if (is_empty(q))
error("큐가 공백상태입니다");
return q->data[q->rear];
}
int main(void)
{
DequeType queue;
init_deque(&queue);
for (int i = 0; i < 3; i++) {
add_front(&queue, i);
deque_print(&queue);
}
for (int i = 0; i < 3; i++) {
delete_rear(&queue);
deque_print(&queue);
}
return 0;
}
--------------
CH.6